Kvantekosmologi med aftagende gravitation
Forening af Mikrokosmos og Makrokosmos
Hubble-parameteren forenet med Universets totale masse
Af Louis Nielsen, cand.scient. i fysik og astronomi
Lektor ved Herlufsholm, Næstved
Indledning
I det følgende en kvante-kosmologi der forener mikrokosmos og makrokosmos og, hvor det antages, at de grundlæggende fysiske størrelser afstand, tid og masse er kvantiserede, dvs. eksisterer i fysiske mindste-størrelser. (Se [1])
En sammenhæng mellem en fysisk mindste afstand, kvantelængden, Universets ’radius’ og fysiske størrelser fra gravitation-teori, elektromagnetisme og kvantemekanik fører til den mulighed, at gravitationskræfterne i Universet til stadighed aftager.
En kosmisk aftagende gravitation kan give en fysisk forklaring på, hvorfor Universet udvider sig.
Formler udledes, der viser, hvordan Newtons gravitations- ’konstant’ aftager med tiden.
Hubbles lov udledes, og det vises at Hubble-parameteren er bestemt ved den relative tidslige aftagen af gravitations-’konstanten’. Ligeledes vises, at Hubble-parameteren har sammenhæng med Universets totale masse og, at den kan udtrykkes som en kvantiseret størrelse.
Kvante-modellen for Universet fører ikke til en ’big-bang singularitet’, som det er tilfældet i standard-kosmologier, der er baseret på Einsteins generelle relativitetsteori.
Rum-tids-kvantisering
I en rum-tids-kvantiseret fysik antages, at der eksisterer fysiske mindste-værdier for afstand og tidsforløb.
Følgende antages at gælde:
Enhver fysisk
afstand
![]() er
lig med et naturligt tal
er
lig med et naturligt tal![]() – rumkvantetallet – multipliceret med en mindste
kvantelængde
– rumkvantetallet – multipliceret med en mindste
kvantelængde
![]() .
Dvs. der gælder:
.
Dvs. der gælder:
(1)
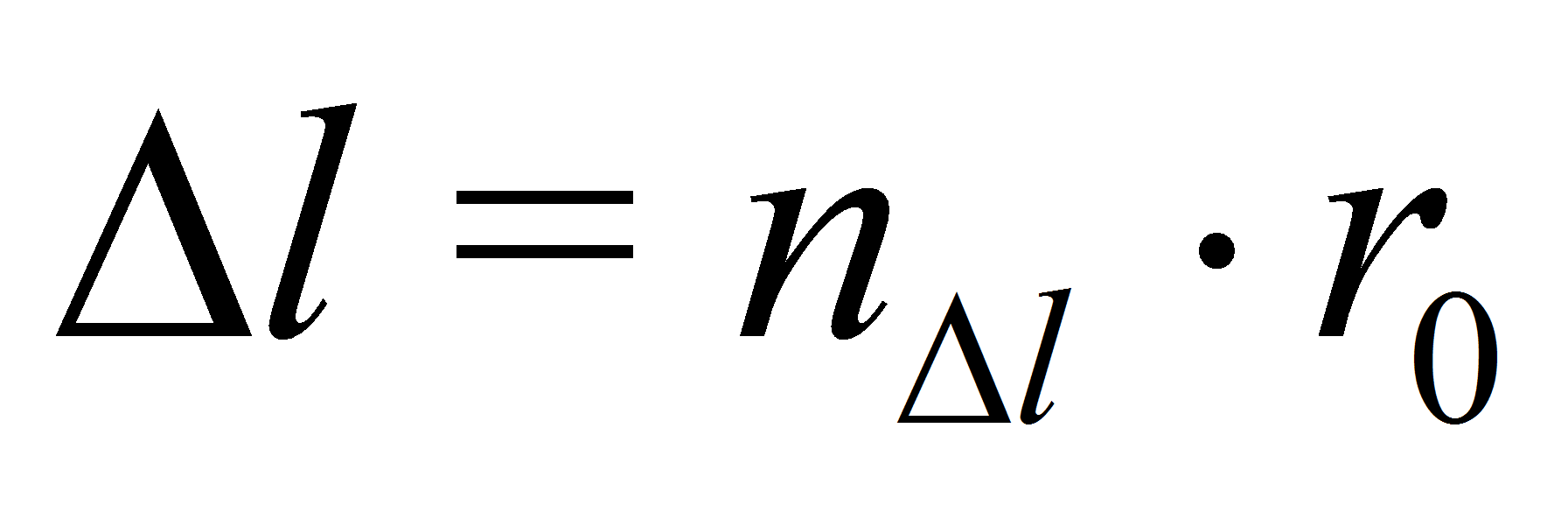
Ethvert fysisk
tidsinterval
![]() er
lig med et naturligt tal
er
lig med et naturligt tal![]() – tidskvantetallet – multipliceret med et mindste
tidsforløb, kvantetiden
– tidskvantetallet – multipliceret med et mindste
tidsforløb, kvantetiden
![]() .
Dvs. der gælder:
.
Dvs. der gælder:
(2)
![]()
Enhver stofportions
masse m antages at være lig med et rationelt tal
![]() – massekvantetallet – multipliceret med Universets totale
masse
– massekvantetallet – multipliceret med Universets totale
masse
![]() .
Dvs. der gælder:
.
Dvs. der gælder:
(3)
![]()
Kosmologiske kvante-størrelser
Alle fysiske størrelser kan udtrykkes ved de fundamentale kvante-kosmologiske størrelser: Kvantelængden, kvantetiden og den totale stof-/energimasse af Universet.
De kosmologiske kvantestørrelser giver mulighed for definition af et absolut kosmologisk måle-enhedssystem.
En fundamental ’atomisering’ af fysiske størrelser medfører, at alle bevægelser er diskontinuerte, dvs. bevægelser foregår i, som regel, uhyre små ’spring’.
Alle fysiske processer i et system vil være kendetegnet ved diskontinuerte ændringer af systemets fysiske størrelser.
Processer i et fysisk system kan beskrives ved ændringer af visse kvantetal hørende til relevante fysiske størrelser, og for disse kvantetal gælder en række bevarelseslove.
Kvantelængden og kvantetiden
Kvante-længden
![]() defineres ved:
defineres ved:
(4)
![]()
Det fysisk mindste
tidsinterval, kvante-tiden
![]() defineres
ved:
defineres
ved:
(5)
![]()
I ligningerne (4) og
(5) er
![]() Plancks konstant
Plancks konstant
![]() lysets hastighed i vakuum og
lysets hastighed i vakuum og
![]() er
Universets totale og konstante stof-/energimasse.
er
Universets totale og konstante stof-/energimasse.
Kvantelængden er
lig med ’Compton-bølgelængden’ svarende til
massen
![]() .
.
Talværdierne af
![]() og
og
![]() er beregnet med
er beregnet med
![]() (se senere).
(se senere).
Forening af Mikrokosmos og Makrokosmos. Den kosmologiske Kvante-formel
Universets aktuelle
’radius’ R og tilhørende alder T kan
ifølge (1) og (2) udtrykkes ved kvantelængden
![]() og kvantetiden
og kvantetiden
![]() ,
idet følgende antages at gælde:
,
idet følgende antages at gælde:
(6)
![]()
Kvante-tallet
![]() i (6), kaldet ’Det kosmiske Evolutions-kvantetal’,
’tikker’ op gennem de naturlige tal samtidig med at
Universet udvikler sig.
i (6), kaldet ’Det kosmiske Evolutions-kvantetal’,
’tikker’ op gennem de naturlige tal samtidig med at
Universet udvikler sig.
Universet begyndte sin
aktive eksistens da
![]() .
I vor epoke er
.
I vor epoke er
![]() (se
senere).
(se
senere).
Det antages at
Universets yderste stof-/energi-kvanter har bevæget sig med
lysets hastighed
![]() siden det begyndte sin aktive eksistens.
siden det begyndte sin aktive eksistens.
Universets aktuelle
’radius’ R og tilhørende alder T er
da sammenknyttet ved relationen:
![]() .
.
Det kosmiske
evolutions-kvantetal
![]() viser
sig at være bestemmende for det tidsafhængige
styrkeforhold mellem de elektriske kræfter og de
gravitationelle kræfter mellem to elektroner.
viser
sig at være bestemmende for det tidsafhængige
styrkeforhold mellem de elektriske kræfter og de
gravitationelle kræfter mellem to elektroner.
En interessant sammenhæng der forener mikrofysik og makrofysik er følgende ’Kosmologiske formel’:
(7)
![]()
I ligning (7)
angiver![]() styrkeforholdet
mellem de elektriske og de gravitationelle kræfter mellem to
elektroner defineret ved følgende brøkforhold:
styrkeforholdet
mellem de elektriske og de gravitationelle kræfter mellem to
elektroner defineret ved følgende brøkforhold:
(8)
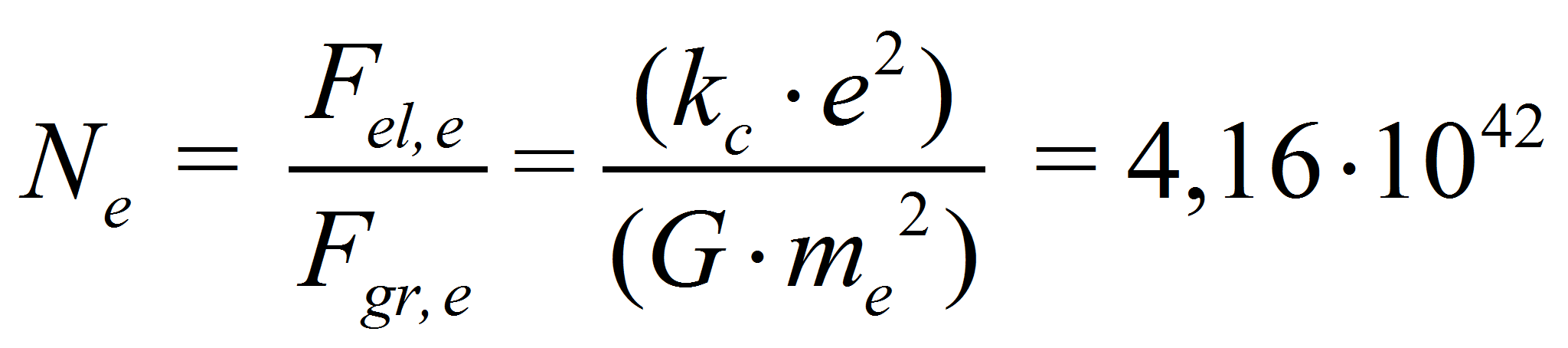
I udtrykket (8) er
![]() Coulombs konstant og
Coulombs konstant og
![]() er den numeriske elektriske ladning af en elektron.
er den numeriske elektriske ladning af en elektron.
Størrelsen![]() er
Newtons gravitations-’konstant’ gældende i vor
epoke.
er
Newtons gravitations-’konstant’ gældende i vor
epoke.
Talværdien af Universets aktuelle ’radius’ R kan beregnes ved hjælp af en målt talværdi af Hubble-parameteren (se senere).
Af ligningerne (6) og
(7) fremgår det at
![]() ,
hvor talværdien er gældende i vor epoke.
,
hvor talværdien er gældende i vor epoke.
Generalisering
Idet det antages, at sammenhængen angivet i (7) ikke kun gælder i vor epoke men også i alle tidligere epoker af Universet, så må det betyde, at en eller flere af de indgående ’naturkonstanter’ i (7) varierer med Universets udvikling. En mulig variabel er Newtons gravitations-konstant G, der er den ældst kendte ’naturkonstant’, men også den ’naturkonstant’, der stadig er målt med mindst nøjagtighed [2].
Nogle forskere mener endog at have målt, at G både kan være tidsafhængig og retningsafhængig.
I det følgende antages, at kun R, T og G varierer med Universets udvikling.
Universets totale masse
Fra ligning (7) kan
Universets totale masse
![]() udtrykkes
ved Universets ’radius’ R:
udtrykkes
ved Universets ’radius’ R:
(9)
![]()
I ligning (9)
fortolkes størrelsen i parentesen
![]() som en fysisk mindste masse af et stof-kvantum, kaldet Uniton. Denne
masse afhænger af Universets til enhver tid aktuelle ’radius’.
som en fysisk mindste masse af et stof-kvantum, kaldet Uniton. Denne
masse afhænger af Universets til enhver tid aktuelle ’radius’.
I vor epoke er
![]() .
.
Kosmisk aftagende gravitation. Kvantisering af G
Af ligningerne (7) og (8) kan vi finde, hvordan G aftager med Universets voksende ’radius’ R og tilhørende alder T. Vi får:
(10)
![]()
I ligning (10) er![]() den ’embryonale gravitations-konstant’, da
gravitations-kræfterne, havde samme styrke som de elektriske
kræfter mellem to elektroner.
den ’embryonale gravitations-konstant’, da
gravitations-kræfterne, havde samme styrke som de elektriske
kræfter mellem to elektroner.
Talværdien af
Universets embryonale gravitationskonstant
![]() er
givet ved:
er
givet ved:
(11)
![]()
Talværdien af![]() er omkring
er omkring
![]() gange
større end gravitations-’konstanten’ i vor epoke.
gange
større end gravitations-’konstanten’ i vor epoke.
Sidste udtryk i (10)
giver en kvantisering af G, hvor ’gravitations-kvantetallet’
er identisk med det kosmologiske evolutions-kvantetal
![]() ,
der ’bestemmer’ udviklingen af G.
,
der ’bestemmer’ udviklingen af G.
I vor epoke er
![]() .
.
Kontinuert matematisk approksimation
Den relative tidsafhængige variation af G er med tidsvariablen T og i en kontinuert matematik givet ved:
(12)
![]()
Talværdien i
ligning (12) er beregnet for vor epoke med
![]() for Universets aktuelle alder (se senere).
for Universets aktuelle alder (se senere).
I den allertidligste udvikling af Universet, aftog gravitationskræfterne uhyre hurtigt.
I de seneste milliarder år er G aftaget uhyre lidt.
Hubbles lov og aftagende gravitation
Hubbles lov kan udledes fra (7) og (12):
(13)
![]()
I ligning (13)
angiver![]() Universets radiale udvidelseshastighed.
Universets radiale udvidelseshastighed.
Hubble-parameteren H(T) er givet ved:
(14)
![]()
Vi ser, at Hubble-parameteren H(T) er en tidsafhængig funktion, der er bestemt ved den relative tidslige variation af G, og at den er omvendt proportional med Universets aktuelle alder T.
Med en målt
talværdi af H(T) i vor epoke kan vi beregne Universets
aktuelle alder T, dets ’radius’ R, dets
totale masse![]() ,
og dermed talværdierne af kvantelængden
,
og dermed talværdierne af kvantelængden
![]() og kvantetiden
og kvantetiden
![]() .
.
Hubble-parameteren
afhænger af
![]()
Den variable
Hubble-parameter H(T) kan udtrykkes ved den totale masse![]() af Universet, lysets hastighed
af Universet, lysets hastighed
![]() ,
Plancks konstant h og brøkforholdet
,
Plancks konstant h og brøkforholdet
![]() ,
hvor G afhænger af T.
,
hvor G afhænger af T.
Der gælder:
(15)
![]()
Af (15) ser vi, at
H(T) afhænger af Universets totale energi
![]() og, at variationen af H(T) har sammenhæng med
variationen af G.
og, at variationen af H(T) har sammenhæng med
variationen af G.
I udtrykket (15) er
Universets totale masse![]() den eneste størrelse man ikke har kunnet måle
talværdien af. Med en målt talværdi af H(T)
kan vi omvendt beregne en talværdi af
den eneste størrelse man ikke har kunnet måle
talværdien af. Med en målt talværdi af H(T)
kan vi omvendt beregne en talværdi af![]() ,
som det er gjort i denne artikel.
,
som det er gjort i denne artikel.
I den her beskrevne kvantemodel antages Universets masse at være en meget fundamental størrelse.
Kvantiseret Hubble-parameter
Ved benyttelse af ’Det
kosmiske Evolutions-kvantetal’
![]() kan Hubble-parameteren udtrykkes som følgende kvante-formel:
kan Hubble-parameteren udtrykkes som følgende kvante-formel:
(16)
![]()
Med
![]() fås:
fås:
(17)
![]()
Det kosmiske
evolutions-kvantetal gennemløber de naturlige tal fra
![]() ,
da Universet begyndte sin dynamiske kvante-udvikling.
,
da Universet begyndte sin dynamiske kvante-udvikling.
I vor epoke er
![]() nået op på det uhyre store tal
nået op på det uhyre store tal
![]() .
.
Kosmologiske kvante-effekter
Vi ser, at
Hubble-parameterens kvante-effekter viste sig mest i det tidligste
Univers, da
![]() gennemløb mindre talværdier.
gennemløb mindre talværdier.
En påvisning af kosmologiske kvante-effekter kan således bedst påvises ved studier af de allerfjerneste objekter i Universet.
Talværdien af Hubble-parameteren
Talværdien af Hubble-parameteren H(T) er siden den blev indført i 1929 af Edwin Hubble (1889-1953) blevet ændret mange gange.
I 2009 er den beregnet
ud fra analyser baseret på målinger med
Hubble-teleskopet. Den beregnede værdi er:
![]() [3].
(1 Mpc = 1 megaparsec)
[3].
(1 Mpc = 1 megaparsec)
Ved at kombinere data
fra forskellige målinger angiver NASA [6] som en
’kompromis-værdi’, der gælder for et ’fladt
univers’:![]() .
.
Universets totale masse, ’radius’ og alder
Ved benyttelse af
talværdien
![]()
kan vi beregne
Universets aktuelle alder T, dets aktuelle ’radius’
R og dets totale masse![]() .
.
Vi får, afrundet:
![]() ;
;
![]() ;
;
![]() .
.
Talværdierne af T og R stemmer med dem man finder i standard kosmologiske modeller.
I ’Standard Kosmologi’ benyttes Universets totale masse ikke som en grundlæggende størrelse, som det er tilfældet her.
Hvad viser målinger
om
![]() ?
?
Astrofysiske observationer og analyser har givet forskellige øvre grænser for, hvor meget G evt. ændrer sig i tiden.
Analyser opnået
ved studier af bl.a. dobbeltpulsarer og Lunar Laser Ranging giver en
øvre grænse for den relative tidslige variation på
![]() (numerisk værdi angivet som
(numerisk værdi angivet som
![]() ).
).
Analyser af type Ia
supernovaer med rødforskydninger på omkring z = 0,5
giver øvre grænser på henholdsvis
![]() og
og
![]() [4].
[4].
Analyser af
pulsations-perioden af den pulserende hvide dværg-stjerne
G117-B15A giver
![]() [5].
[5].
En entydig øvre
grænse for
![]() er således ikke påvist.
er således ikke påvist.
En god oversigtsartikel fra 2002, der gør status om mulige variationer af naturkonstanterne, herunder også G, findes i [7].
Aftager den kosmiske gravitation?
Den her fremlagte kvantekosmologi hævder, at de gravitationelle kræfter i Universet er stadig aftagende. Den teoretiske talværdi for den relative variation af G angivet i ligning (12) ligger i nærheden af de grænser som forskellige astrofysiske analyser har givet.
Da talværdien af G kun er målt med få betydende cifre, ja, så kan det endnu ikke ultimativt afgøres om G varierer eller er konstant.
Først når meget følsomme gravimetre med stor nøjagtighed har målt, over flere år og på mange forskellige steder af Jordens overflade, de lokale tyngdeaccelerationer vil det være muligt at afgøre om G varierer.
Hvis man ud fra gravimetriske målinger vil beregne en evt. ændring af G, så skal der kompenseres for bl.a. gravitationelle tidekræfter fra specielt Månen og Solen. Disse bevirker, at Jordens rotation bremses, og dette formindsker centrifugal-accelerationer. Og, i længden, giver det en mindre fladtrykning af Jorden, således at forholdet mellem Jordens polradius og ækvatorradius ændres.
Hvis G er en aftagende størrelse, ja, så kan det tyde på, at gravitationskræfter forårsages at et kosmisk stofligt medium med en tæthed der til stadighed aftager.
Kvante-universet ved Planck-tiden. Planck-massen forklaret
Den her fremlagte
model af Universets kvante-udvikling kan beregne forhold før
og ved den såkaldte Planck-tid på omkring
![]() .
Modellen kan beregne følgende:
.
Modellen kan beregne følgende:
Da Universet havde en
’radius’ lig med Planck-længden
![]() og
en alder lig med Planck-tiden
og
en alder lig med Planck-tiden
![]() ,
da bestod det af omkring
,
da bestod det af omkring
![]() stof-kvanter
(unitoner), hver med en masse lig med Planck-massen på
stof-kvanter
(unitoner), hver med en masse lig med Planck-massen på
![]() .
.
Den relativt store talværdi af Planck-massen har hermed en mulig forklaring (Mere i [1]).
Den Kosmiske Embryoton. Universets kvanteudvikling
De foregående teoretiske resultater fører til spørgsmålet:
Hvordan begyndte Universet sin eksistens og udvikling?
Muligvis som følger:
Alt stof og energi i Universet var i begyndelsen koncentreret i den Kosmiske Embryoton, betegnelsen for en uhyre lille ’foster-partikel’ med en udstrækning svarende til den fysisk mindste udstrækning, kvante-længden.
Den kosmiske embryoton tillægges en konstant masse lig med den totale konstante masse af det til enhver tid udviklede Univers.
Universets dynamiske kvante-udvikling kan tænkes at være foregået ved successive delinger af den oprindelige kosmiske embryoton. De dannede stof-/energi-kvanter, kaldet Unitoner, har siden ved desintegrationer og kombinationer dannet alle de ’partikler’, der eksisterer i det aktuelle Univers.
Evolution af Naturlovene?
Samtidig med Universets ’fødsel’ udvikledes de første Naturlove - i ’kvantespring’. Den første Naturlov var entropiloven (forandringsloven). Denne lov ’bevirker’, at et system forandrer sig fra en mindre sandsynlig tilstand til en mere sandsynlig tilstand.
Universet udvikler sig generelt fra mere ordnede og kompakte tilstande til opdelte og mindre ordnede tilstande.
Gravitationskræfterne
’fødtes’ med en styrke, der var omkring
![]() gange større end i dag. Med en stadig aftagende styrke vil
gravitationskræfterne kunne opfylde entropiloven.
gange større end i dag. Med en stadig aftagende styrke vil
gravitationskræfterne kunne opfylde entropiloven.
Man kan stille spørgsmålet: Er de forskellige Naturlove ’opstået’ og har ændret sig efterhånden som Universet har udviklet sig?
Det absolutte kosmologisk embryonale koordinat-system
Den Kosmiske Embryoton giver os mulighed for at definere et abstrakt matematisk og absolut reference-system med et absolut centrum for det udviklende Univers.
Positioner og bevægelsesforhold for alle dannede stof-/energi kvanter kan, i princippet, henføres og beregnes i forhold til det embryonale kosmologiske koordinatsystem, som vi kan kalde det kosmologiske embryoton-system eller det kosmologiske absolutsystem.
Litteratur
[1] Louis Nielsen, http://louis.rostra.dk
[2] CODATA: http://www.physics.nist.gov/cgibin/cuu/Value?bg
[3] Adam Riess, http://hubblesite.org/newscenter/archive/releases/2009/08/full
[4] E. Gaztañaga et al. Physical Review D, 65, 1 (2001)
[5] Marek Biesiada, Beata Malec, Mon. Not. Roy. Astron. Soc. 350, 644 (2004)
[6] NASA, http://wmap.gsfc.nasa.gov/universe/uni_expansion.html
[7] Jean-Philippe Uzan, http://xxx.lanl.gov/abs/hep-ph/0205340
Louis Nielsen
3. august 2009