|
Indledning I det følgende vil jeg vise, at der eksisterer en sammenhæng mellem energitilstandene i et hydrogenatom og universets totale energiindhold. Det vises, at den mekaniske energi af en elektron i en bestemt tilstand er lig med en bestemt brøkdel af universets totale energi. Det vises, at de diskontinuerte egenskaber er en konsekvens af rummets, tidens og massens kvantisering.
I 1913 viste Niels Bohr (Niels Bohr (1885-1962): 'On the Constitution of
Atoms and Molecules', Philosophical Magazine, 26, 1 (1913)),
hvordan man kunne få kvantiseret energien i et H-atom, og
således give en kvantitativ »forklaring« af de
eksperimentelle data, der vedrører H-atomets linjespektrum.
For at få kvantiseret energimulighederne i H-atomet antog Bohr
ad hoc, at elektronens impulsmoment, dvs. produktet af dens masse,
hastighed og afstand fra protonen var lig med et naturligt tal
multipliceret med Plancks konstant divideret med 2
(1) 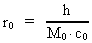
hvor h er Plancks konstant, c0 lysets hastighed og M0 universets totale stof-/energimasse. (2) 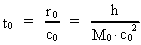
I en rationel kvantefysik gælder: Enhver fysisk endelig afstand 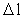 er et naturligt
tal – rumkvantetallet er et naturligt
tal – rumkvantetallet 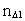 multipliceret med elementarlængden r0. Dvs. der
gælder:
multipliceret med elementarlængden r0. Dvs. der
gælder:
(3) 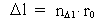
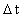 er lig med et naturligt
tal – tidskvantetallet er lig med et naturligt
tal – tidskvantetallet 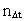 multipliceret med elementartiden t0. Dvs. der gælder:
multipliceret med elementartiden t0. Dvs. der gælder:
(4) 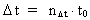
Processer i et fysisk system kan beskrives ved ændringen af visse kvantetal hørende til bestemte fysiske størrelser. Alle fysiske størrelser kan udtrykkes ved de kosmiske fundamentalstørrelser: Rumkvantet, tidskvantet og den totale masse af universet!
Hastighed og acceleration i den diskontinuerte bevægelse (5) 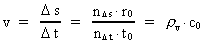
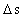 er den strækning, der
tilbagelægges i tidsintervallet er den strækning, der
tilbagelægges i tidsintervallet
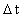 . I definitionsligningen (5) er . I definitionsligningen (5) er
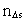 rumkvantetallet hørende til
afstanden rumkvantetallet hørende til
afstanden 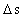 og og
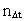 tidskvantetallet hørende
til tidsintervallet tidskvantetallet hørende
til tidsintervallet 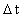 .
Brøkforholdet mellem disse to kvantetal definerer et
rationelt hastighedskvantetal, betegnet med .
Brøkforholdet mellem disse to kvantetal definerer et
rationelt hastighedskvantetal, betegnet med
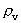 . Dette hastighedskvantetal ligger
i talintervallet mellem nul og en, idet en partikels hastighed aldrig må overstige c0. . Dette hastighedskvantetal ligger
i talintervallet mellem nul og en, idet en partikels hastighed aldrig må overstige c0.
Hvis en partikel ændrer sin hastighed inden for et bestemt tidsinterval, siges partiklen at accelerere. Accelerationens størrelse a defineres ved følgende udtryk: (6) 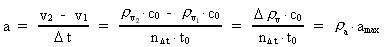
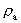 accelerationskvantetallet,
der ses at være et rationelt tal, der ligger i talintervallet fra nul til en. Brøkforholdet mellem lyshastigheden og elementartiden c0/t0 giver en teoretisk fysisk øvre grænse for en partikels acceleration. Denne øvre grænse betegnes med amax. accelerationskvantetallet,
der ses at være et rationelt tal, der ligger i talintervallet fra nul til en. Brøkforholdet mellem lyshastigheden og elementartiden c0/t0 giver en teoretisk fysisk øvre grænse for en partikels acceleration. Denne øvre grænse betegnes med amax.Hvis det – i et bestemt referencesystem – registreres, at en partikel har en acceleration, da siger vi, at den er påvirket af en kraft.
Elektronens kvanteenergi i hydrogenatomet
Elektronens kvanteenergi (7) 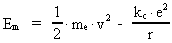
For at elektronen kan bevæge sig i en lukket bane skal den være påvirket af en 'centripetalkraft' rettet ind mod protonen. Denne kraft udøves af den tiltrækkende elektriske coulombkraft fra protonen. Vi kan således opskrive Newtons 2. lov for elektronens bevægelse sådan: (8) 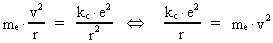
(9) 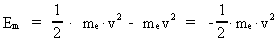
(10) 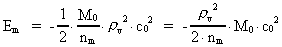
(11) 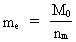
(12) 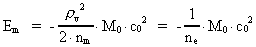
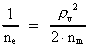 Af ligning (12) ser vi følgende: Elektronens kvanteenergi i en bestemt kvantebane er lig med en bestemt brøkdel af universets totale energi, hvilket er en logisk rimelighed. At energien er negativ viser, at elektronen er i en 'bunden' kvantebane, og i øvrigt er fortegnet bestemt af valget af nulpunkt for den elektrisk potentielle energi.
Da lyskonstanten c0 er lig med forholdet mellem
elementarlængden og elementartiden, ser vi følgende af
ligning (12): Atomets kvanteenergi er bestemt af elementarlængden,
elementartiden og universets totale masse. Dertil kommer et
systemafhængigt kvantetal. I ligning (12) er ne atomets
kosmiske energikvantetal.
Da universets totale masse er omkring 1,6 · 1060 kg (se
min kvantekosmologi), altså et uhyre
stort tal, er det kosmiske energikvantetal også et uhyre stort tal,
af størrelsesordenen 1095. Praktisk regning med
sådanne store tal er omstændelig, så derfor kan vi
af praktiske grunde igen indføre hvilemassen af en elektron i
ligning (12).
Kvantefysisk udledning af Rydbergformlen (13) 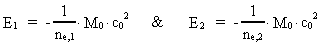
(14) 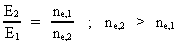
(15) 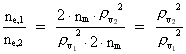
Vi kan nu udtrykke forholdet mellem disse hastighedskvantetal ved rumkvantetal, der kun kan antage naturlige tal, dvs. 1, 2, 3, ... osv. Hvis en elektron befinder sig i den højere energitilstand E2, vil den i et kvantespring 'søge' ned til den lavere energi E1. Under denne proces skal der gælde impulsmomentbevarelse, dvs. produktet af elektronens masse, hastighed og afstand fra kraftcentret skal være konstant. Der skal altså gælde; idet det antages, at en foton udsendes 'radiært': (16) 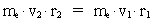
Udtrykkes hastighederog afstande ved de kvantiserede størrelser, fås: (17) 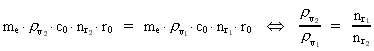
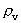 er hastighedskvantetallet, og nr er rumkvantetallet. Benyttes dette udtryk i ligning (15), får vi: er hastighedskvantetallet, og nr er rumkvantetallet. Benyttes dette udtryk i ligning (15), får vi:
(18) 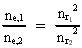
(19) 
(20) 
Hvis en elektron overgår fra eksempelvis den højere energitilstand E2 til den lavere energitilstand E1, vil energiforskellen blive udsendt som en foton. Da disse to energitilstande svarer til rumkvantetallene nr1 = 1 og nr2 = 2, kan vi skrive: (21) 
Den numeriske værdi af E1 er lig med ioniseringsenergien, dvs. den positive energi, der skal tilføres atomet for at løsrive en elektron fra energitilstanden E1. For at kunne beregne atomets energitilstande kræves blot en måling af atomets ioniseringsenergi. Vi kan nu skrive (21) på en generel måde, svarende til rumkvantetallene nr1 og nr2. Der gælder: (22) 
Ligning (22) er formelt identisk med de formler, som Balmer og Rydberg fandt frem til på rent empirisk grundlag, idet de ikke kunne begrunde dem som en konsekvens af fundamentale fysiske forhold i vort univers. Det skal bemærkes, at de foregående udledninger er baseret på 'punktladninger', og dette resulterer i ikke-realistiske geometriske forhold. I en mere realistisk model må man tage hensyn til partiklernes udstrækning, hvilket giver et andet matematisk udtryk for Coulombenergien. Ligeledes må man tage hensyn til de magnetiske energiforhold, der forårsages af elektronens og protonens henholdsvis banebevægelse og spinbevægelse. Hvis disse energibidrag medtages i beregningerne, vil man også kunne redegøre for hydrogenspektrets såkaldte finstruktur og hyperfinstruktur.
Til slut vil jeg igen betone, at de foregående udredninger skal vise, at
kvanteaspekterne i vort univers er forårsaget af den fundamentale kvantisering af
rum, tid og masse, og at denne kvantisering er bestemt af vort univers'
endelige masse. »Delen er bestemt af helheden!« — »Det
mindste er bestemt af det største!« 2/1-1997
Louis Nielsen
|
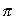 .
Ved hjælp af denne ad hoc-antagelse kunne Bohr udlede en
energiformel, der var kvantiseret, dvs. elektronen kan kun have ganske
bestemte og adskilte energitalværdier. Nu er det imidlertid
sådan, at den fysiske størrelse, som vi kalder impulsmoment,
er afledt af de fundamentale fysiske størrelser: afstand,
tidsinterval og masse, hvilket også er tilfældet for
alle andre fysiske størrelser!
Som følge af dette er det rimeligt at formode, at kvantiseringen
allerede er til stede på dette fundamentale niveau!
.
Ved hjælp af denne ad hoc-antagelse kunne Bohr udlede en
energiformel, der var kvantiseret, dvs. elektronen kan kun have ganske
bestemte og adskilte energitalværdier. Nu er det imidlertid
sådan, at den fysiske størrelse, som vi kalder impulsmoment,
er afledt af de fundamentale fysiske størrelser: afstand,
tidsinterval og masse, hvilket også er tilfældet for
alle andre fysiske størrelser!
Som følge af dette er det rimeligt at formode, at kvantiseringen
allerede er til stede på dette fundamentale niveau!