|
Comptoneffekten
Af Lektor cand.scient. Louis Nielsen, Herlufsholm
Indledning I det følgende vil jeg give en alternativ udledning af masseenergiformlen og masseforøgelsesformlen og ligeledes forsøge at give disse formler en fysisk-mekanisk forståelse. Masseenergiformlen sammenknytter et systems masse med dets totale energiindhold. En sådan formel blev i 1905 udledt af Albert Einstein i den specielle relativitetsteori. Formlen udsiger, at et systems totale energiindhold er lig med systemets inertielle masse ganget med lyshastigheden i anden potens. En dybere fysisk forståelse haves ikke i den kendte fysik, så i mangel af denne antager man, at masseenergi er en fundamental energiform, der ikke kan reduceres til noget mere fundamentalt. En konsekvens af min holistiske kvantekosmologi er eksistensen af nogle mindste stof-/energi-kvanter som jeg har givet navnet unitoner. En given partikels – dvs. et subsystem der består af mere end en uniton - masseenergi kan meget vel være lig med den totale kinetiske energi af de unitoner som partiklen består af. Masseforøgelsesformlen udsiger, at en partikels inertielle masse forøges med partiklens hastighed. En sådan formel blev i 1905 udledt af Albert Einstein i den specielle relativitetsteori. Forsøg udført af bl.a. W. Kaufmann i 1901 og af A.H. Bucherer i 1908 (Bucherer A.H. , Verh.deutsch.phys. Ges. Vol. 6 (1908)) viste, at den inertielle masse tilsyneladende blev forøget med forøget hastighed i overenstemmelse med følgende formel: (1) 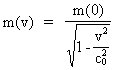
hvor m(v) er partiklens inertielle masse ved hastigheden v, m(0) hvilemassen,
dvs. massen ved hastigheden 0, og c0 er lysets hastighed i
såkaldt vacuum.
I mine udledninger af masseenergiformlen og masseforøgelsesformlen
benytter jeg Newtons 2. lov, der definerer størrelse og retning af
den såkaldte resulterende kraft Fres. Endvidere
benyttes definitionsformlen for størrelsen af det arbejde
dAres, som en kraft Fres udfører på en
partikel over en lille forskydning ds, og i forbindelse hermed definitionen
af en partikels tilvækst i kinetisk energi dEk. (2) 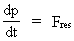 (3) 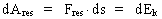 Ligning (2) definerer størrelsen Fres af den resulterende kraft som den tidslige tilvækst af en partikels impuls p. Impulsen p af en partikel er defineret ved produktet af partiklens øjeblikkelige inertielle masse m(v) – der, som forsøg viser, antages at afhænge af hastigheden – og dens øjeblikkelige hastighed v, dvs: (4) 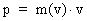
Ligning (3) angiver definitionen af den resulterende krafts arbejde på
en partikel over strækningen ds, og angiver, at dette arbejde definerer
tilvæksten i partiklens kinetiske energi. (5) 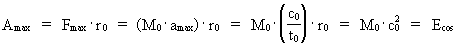
hvor M0 er universets samlede masse, og t0 er lig
med elementartiden. c0/t0 = amax
er en øvre talværdi for acceleration, og r0/t0 =
c0. M0·amax = Fmax
ifølge Newtons 2. lov. (6) 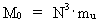
hvor N angivet det aktuelle forhold mellem de elektrostatiske og de
gravitostatiske kræfter mellem to elektroner, eller forholdet mellem
talværdien af Newtons gravitations’konstant’ da universet blev
’født’ og talværdien i vor epoke. (7) 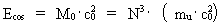
Da unitonerne er de mest fundamentale fysiske enheder i universet, og da de
ikke har en indre struktur og er udelelige (de sande atomer)
må størrelsen (mu·c02)
være lig med en kinetisk energiform! En energiform der skyldes unitonens
bevægelse. (mu·c02) må
være lig med den totale kinetiske energi af én
uniton!! Alt stof – elektroner, protoner etc. – og også
såkaldt vacuum antages at bestå af unitoner, og alle virkninger
forestilles at være et resultat af unitonernes bevægelses- og
sammenstødsforhold. (8) 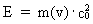 Ved benyttelse af ligning (4) kan E også skrives som: (9) 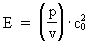 Vi vil nu bestemme funktionsudtrykket for m(v). Udtrykket i (3) kan omformes til: (10) 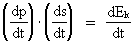
Da (11) 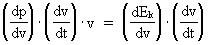 Ligning (11) kan omkrives yderligere til: (12) 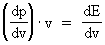
hvor E = Ek + m(0)·c02 er partiklens
totale energi, og m(0)·c02 er partiklens
hvilemasseenergi, der antages konstant. (13) 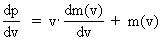 og (14) 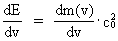 Indsættes udtrykkene i (13) og (14) i (12) fås følgende differentialligning til bestemmelse af m(v): (15) 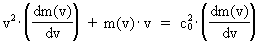 Ligning (15) omskrives til: (16) 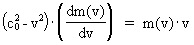 og dernæst kan de variable separeres: (17) 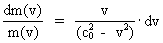 Ligning (17) kan integreres til følgende: (18) 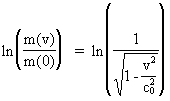 hvor ln er den naturlige logaritmeoperator. Af (18) får vi masseforøgelsesformlen: (19) 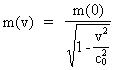
Af (19) ser vi, at der matematisk gælder, at m(v) går mod
uendelig, når v går mod c0, men fysisk kan
massen maximalt blive lig med universets samlede masse! Dette kommer jeg
tilbage til. Den kinetiske energi af en partikel Ek kan beregnes af: (20) 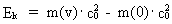
Hvis c0 er ens for alle iagttagere i forskellige inertialsystemer,
vil det være muligt at udlede alle ligningerne i den specielle
relativitetsteori, eksempelvis Lorentztransformationsligningerne.
Ifølge min teori er c0 givet ved forholdet mellem
elementarlængden r0 og elementartiden t0, og da
disse elementarstørrelser er invariante over for en vilkårlig
koordinattransformation, vil c0 også være det. (21) 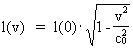 Af (21) ser vi, at der matematisk gælder, at l(v) går mod nul, når v går mod c0, men den fysisk mindste længde, som l(v) kan have, er lig med elementarlængden r0!
En given partikels masse kan aldrig blive fysisk større end den totale
masse af universet M0 og ej heller mindre end den aktuelle masse
af en uniton. Ligeledes kan udstrækningen af partiklen principielt
aldrig blive større end universets aktuelle udstrækning og ej
heller mindre end elementarlængden. Hvis vi benytter disse grænser
i masseforøgelsesformlen (19) og længdeforkortningsformlen (21),
er det muligt at udlede formeludtrykket for en partikels såkaldte
compton’bølgelængde’. (22) 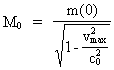 og: (23) 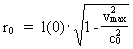 Ved isolation af vmax i henholdsvis (22) og (23) fås: (24) 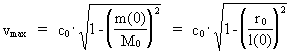 Vi ser af (24), at en partikels hastighed aldrig kan nå op på eksakt c0. Af (24) eller direkte ved at gange (22) og (23) sammen får vi følgende sammenhæng: (25) 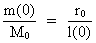 eller: (26) 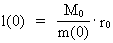 Elementarlængden r0 har følgende sammenhæng med Plancks konstant h, M0 og c0: (27) 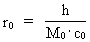 Benyttes (27) i (26) fås: (28) 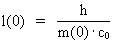
Formel (28) er identisk med den såkaldte
compton’bølgelængde’formel, her dog fremkommet på en
anden måde end sædvanlig. (Referencer: A.H.Compton, ’The Spektrum of Scattered X-rays’, Physical Review vol.22, (1923) og ’A Quantum Theory of the Scattering of X-rays by Light Elements’, Physical Review, vol. 21, (1923)). © Louis Nielsen, februar 1998
|
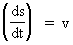 fås:
fås: