|
The Motion of a Photon in a
gravitostatic Field
otherwise analyzed than in Einstein's theory of gravitation
By Louis Nielsen, Senior Physics Master, M.Sc.
Introduction
In the following I shall show that it is possible, by means of the Newtonian
mechanics and quantum physical equations valid for a photon, to arrive at
equations which are in conformity with equations deducted in Einstein's
general theory of relativity. We shall consider the motion of a photon in
a gravitostatic field. We find that both the velocity of the photon and the
"dualistic" wavelength belonging to it depend on the gravitational
field.
Motion of a photon in a gravitostatic field
Let us consider a spherical symmetric active gravitational mass m, which
in the distance r from its center creates a
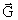 -field given by: -field given by:
(1) 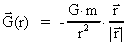
where G is Newton's gravitational constant. The equation of motion for the
photon is given by Newton's 2nd law:
(2) 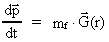
where 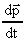 is the
increase in momentum per time, and mf is its gravitational mass,
which according to Einstein's equivalence principle is equal to its
inertial mass. is the
increase in momentum per time, and mf is its gravitational mass,
which according to Einstein's equivalence principle is equal to its
inertial mass.
The particle quantities 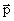 and mf we shall express by the dualistic wavelenth of the photon.
and mf we shall express by the dualistic wavelenth of the photon.
Let us use the expression a field free vacuum; hereby we mean a domain
of space absolutely free from both fields and matter.
If we consider a photon in such field free vacuum, then its velocity in a given
frame of reference will be equal to the characteristic constant, c0,
which a.o. is used in the equations of the special theory of relativity.
If a photon is situated within a field, it is unlikely that it has the
velocity c0, but another velocity c.
A photon moving in field free vacuum will have a total energy
E0 given by:
(3) 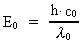
where h is Planck's Constant and 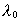 the wavelength of the photon. If the photon as an example moves into a
gravitational field, it will have an energy E which we can write as:
the wavelength of the photon. If the photon as an example moves into a
gravitational field, it will have an energy E which we can write as:
(4) 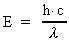
where c is the velocity in the field and
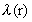 its
wavelength in the field. its
wavelength in the field.
Assuming that the energy of the photon during the motion is constant, we get:
(5) 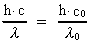
viz. the ratio between the velocity and the wavelength of the photon is
constant, in spite of the fact that each of them may vary. As
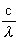 gives the frequency,
this is seen to be constant. gives the frequency,
this is seen to be constant.
The inertial mass, and thereby the gravitational mass, we can get from
Einstein's energy-mass relation:
(6) 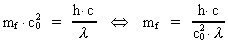
As 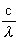 is constant,
we see that the photon retains a constant mass, even if its velocity is
changing. This is not the case for particles of "matter", as
their inertial mass increases with the velocity. The momentum p of the photon
is given by: is constant,
we see that the photon retains a constant mass, even if its velocity is
changing. This is not the case for particles of "matter", as
their inertial mass increases with the velocity. The momentum p of the photon
is given by:
(7) 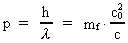
By using (6) and (7) we can rewrite the equation of motion for the photon
in a 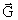 -field, considering a radial movement: -field, considering a radial movement:
(8) 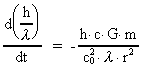
As 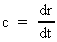 (8) can be rewritten to: (8) can be rewritten to:
(9) 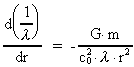
where the expression from equation (7) has been inserted.
Separating the variables 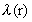 and r
we get: and r
we get:
(10) 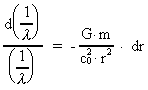
Equation (10) can be integrated as:
(11) 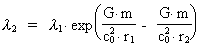
where a < r1 < r2 is the distance to two points,
measured from the center of the gravitating mass m, which is assumed to be
spherical symmetric with radius a. 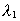 and and
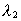 are the wavelengths of the photon,
corresponding to r1 og r2. are the wavelengths of the photon,
corresponding to r1 og r2.
If we let r2 increase towards "infinity", corresponding
to a field free domain with the wavelength
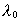 , we can write: , we can write:
(12) 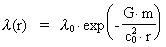
where 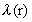 is the wavelength
corresponding to the distance r. is the wavelength
corresponding to the distance r.
As 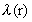 and c have a constant ratio,
the following equation is valid for the velocity of the photon c(r) in
a distance r from the gravitating mass: and c have a constant ratio,
the following equation is valid for the velocity of the photon c(r) in
a distance r from the gravitating mass:
(13) 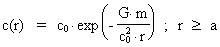
If 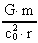 is considerably below 1,
which is the case for most objects, we can with reasonably good precision use
development to the first order of the series. Then we get the following
expressions for is considerably below 1,
which is the case for most objects, we can with reasonably good precision use
development to the first order of the series. Then we get the following
expressions for
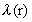 and c(r) : and c(r) :
(14) 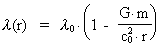
(15) 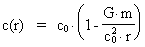
Equation (12) shows that a photon moving in a gravitational field is
"exposed" to a change of wavelength together with a change of
velocity. The velocity of a photon as function of its distance from the
gravitating mass m is given by equation (13).
Gravitational shift of the wavelength
Let us calculate the relative change of wavelength corresponding to two
distances r1 and r2, using the expression from
equation (14). We get:
(16) 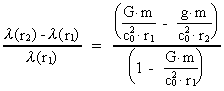
where 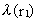 is the wavelength at the
distance r1, and is the wavelength at the
distance r1, and 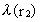 is the wavelength at the distance r2.
is the wavelength at the distance r2.
If a photon is emitted from f.i. the surface of the Sun, where r1
~= 7 · 108 m, and the wavelength of this
photon is measured at the surface of the Earth, where r2
~= 1,5 · 1011 m, then we get, with a solar
mass m = 2 · 1030 kg and r2 >> r1:
(17) 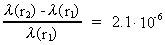
This value is in agreement with the actually measured change of wavelength
and is the same as deducted in Einstein's general theory of relativity,
however with the difference that the latter theory operates with the
frequency and not the wavelength. (See f.i. C. Møller: The Theory of
Relativity, Oxford, 1952, p. 346).
Velocity of light in the general theory of relativity
The general theory of relativity deducts an equation for the velocity of
"light" in a gravitational field (see f.i. C. Møller, p. 353).
This equation is:
(18) 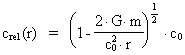
where we note a square root, contrary to the exponential function in equation
(13).
If (18) is developed to the 1st order, it will be identical to (15). In (18)
there is a critical distance rs given by:
(19) 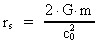
The distance is called Schwarzschilds's radius and indicates in which
distance the velocity of light becomes zero. If r < rs,
crel(r) becomes imaginary, which gives non-physical conditions.
The conception "black hole" is defined as an object with its mass
concentrated within the distance r < rs. In equation (13)
there are no critical distances, making it more physical than equation (18).
Bending of light around a gravitating mass
What made Einstein famous was an "apparent" confirmation of a
phenomenon he had predicted by his general theory of relativity.
Einstein calculated that a light beam, passing near to the Sun, would be
bent 1.75 arc seconds. Half of this bending was caused by a change of the
velocity of light, calculated according to equation (18). The second half
was determined by the "curvature" of space, which was determined
by the quantity of the present gravitational mass. This "curvature"
of space can be calculated from Einstein's "geometrical" field
equations.
At a solar eclipse in 1919 Arthur Eddington arranged an expedition to a
place where this eclipse would be total. During the "totality"
of the eclipse photographs were taken of the eclipse and surrounding stars,
of which there were only few. Comparing the pictures with a photography of
the same area of the sky, but without the Sun, a bending could be established.
The analyses, however, were primitive and with great variations in the
measured bendings.
A gravitational bending also follows from equation (13), which I have
deducted, but using this equation we get a bending of 0.87 arc seconds
caused by the Sun.
A further bending is caused by the gravitational rotation field
(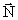 -field), which is present around all
gravitating masses in relative motion. As the Sun rotates, this will cause an -field), which is present around all
gravitating masses in relative motion. As the Sun rotates, this will cause an
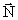 -field, which will produce a force on every
gravitational mass, moving within the field. The -field, which will produce a force on every
gravitational mass, moving within the field. The
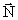 -field shall be calculated from the
gravitational field equations, as I have explained in my article:
A Maxwell Analog Gravitation Theory
with two gravitational fields. -field shall be calculated from the
gravitational field equations, as I have explained in my article:
A Maxwell Analog Gravitation Theory
with two gravitational fields.
Next article
Main entry
| 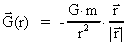
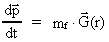
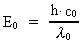
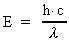
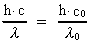
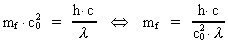
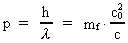
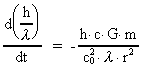
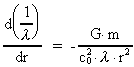
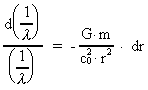
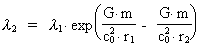
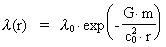
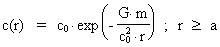
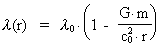
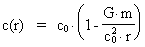
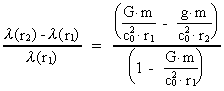
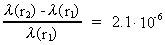
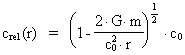
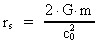
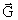 -field given by:
-field given by:
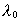 the wavelength of the photon. If the photon as an example moves into a
gravitational field, it will have an energy E which we can write as:
the wavelength of the photon. If the photon as an example moves into a
gravitational field, it will have an energy E which we can write as:
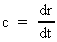 (8) can be rewritten to:
(8) can be rewritten to:
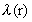 and r
we get:
and r
we get:
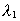 and
and
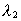 are the wavelengths of the photon,
corresponding to r1 og r2.
are the wavelengths of the photon,
corresponding to r1 og r2.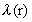 is the wavelength
corresponding to the distance r.
is the wavelength
corresponding to the distance r.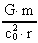 is considerably below 1,
which is the case for most objects, we can with reasonably good precision use
development to the first order of the series. Then we get the following
expressions for
is considerably below 1,
which is the case for most objects, we can with reasonably good precision use
development to the first order of the series. Then we get the following
expressions for
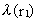 is the wavelength at the
distance r1, and
is the wavelength at the
distance r1, and 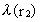 is the wavelength at the distance r2.
is the wavelength at the distance r2. -field), which is present around all
gravitating masses in relative motion. As the Sun rotates, this will cause an
-field), which is present around all
gravitating masses in relative motion. As the Sun rotates, this will cause an