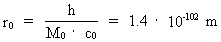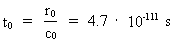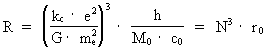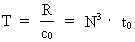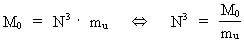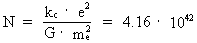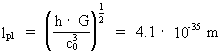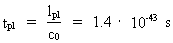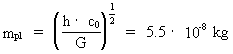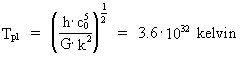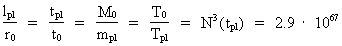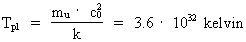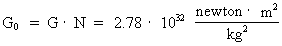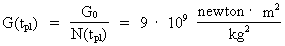Introduction
The socalled Planck units are not based on a physical theory, and neither are they themselves base for a physical theory. They are 'constructed' purely ad hoc by a dimension analysis, based on Newton's gravitational constant, the velocity of light and Planck's constant. The intention of Max Planck was – in 1899 – to find a unit of length, a unit of time and a unit of temperature, independent of specific local systems and the existence of man.
Reference: Max Planck: 'Über irreversible Strahlungsvorgänge'. Sitzungsberichte der Preußischen Akademie der Wissenschaften, vol. 5, p. 479 (1899).
Most cosmologists, trying to describe the earliest phases of our universe by a Big Bang model, use the Planck time unit, about 10^-43 sec, as the nearest possible time which can be used to approach the 'moment' of Big Bang. Events before the Planck time cannot be described by the conventional cosmological theories. Einstein's general theory of relativity, which is basical for the accepted cosmological models, collapses when somebody tries to analyse the early Universe. The reason is a.o. that the theory is not based on quantum physics.
The cosmological quantum units, discovered by me, elementary length, elementary time and elementary mass, which are basical for my holistic quantum cosmology (see this), are as such much more fundamental than the Planck units. In the following I shall show the context between my quantum cosmological units and the Planck units, and furthermore I shall show which role the Planck units play in my holistic quantum cosmology. I shall give an explanation of the socalled Planck mass, which is about 5.5·10^-8 kg, and the socalled Planck temperature, about 10³² kelvin. Especially what the relatively great Planck mass concerns, it has until now been an enigma. In the following I shall give the solution.

Elementary length, elementary time, elementary mass and the Planck units
Basical for my holistic quantum cosmology is the existence of a smallest physical length, elementary length r₀, a smallest physical time interval, elementary time t₀ and a smallest physical mass, elementary mass m_u.   r₀ and t₀ are given by:

(1)

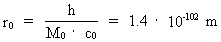
and

(2)

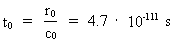
where h = 6.63·10^-34 J·s is Planck's constant, c₀ = 3·10⁸ m/s is the velocity of light, and M₀ = 1.6·10⁶⁰ kg is the total matter/energy mass of the Universe, as calculated in my holistic quantum cosmology. The mass of the Universe is an utterly fundamental quantity, determining both local as well as cosmological-physical states. This interaction between local and cosmical we can call the holistic principle.

Some fundamental equations in my holistic quantum cosmology are the following cosmological basic equations, where it should be noted that the equations (4) and (5) are deducted from equation (3), which could be called the holistic formula as it connects physical quantities from microcosmos and macrocosmos:

(3)

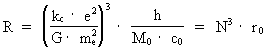
(4)

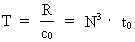
(5)

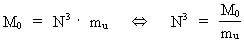
where R is the actual extension of the Universe, k_c = 9 · 10⁹ (newton·m²)/ coulomb² is Coulomb's constant, m_e = 9.11 · 10^-31 kg the mass of the electron, e = 1.6 · 10^-19 coulomb its electrical charge, G Newton's gravitational 'constant' and T the actual age of the Universe.   m_u is the actual mass of the physically smallest matter/energy quantum, elementary mass, when the extension of the Universe is R and its cosmic age T. This physically smallest matter/energy quantum I have given the name a uniton. N is the ratio between the electrostatical and gravitostatical forces between two electrons, and is given by:

(6)

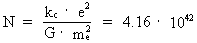
in our epoch of the evolution of the Universe.

N³ plays the role as a cosmic evolution quantum number, which had the value 1 (one) when the Universe was 'born'. From equation (5) we see that N³ is equal to the number of unitons in the Universe, when the extension is R and its age is T.
When the Universe was 'born' it consisted of one quantum – the cosmic embryoton. Gradually as the evolution quantum number was 'ticking' up through the natural numbers, the original cosmical embryoton disintegrates in more and more elementary quanta – unitons. In our epoch there are about 7.2 · 10¹²⁷ unitons. As I assume that the mass of the Universe – during its whole existence – is constant, this means that the mass of a uniton decreases gradually as the Universe expands.

The Planck length l_pl, the Planck time t_pl, the Planck mass m_pl and the Planck temperature T_pl are given by the following expressions:

(7)

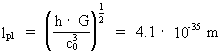
(8)

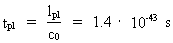
(9)

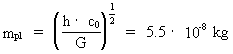
(10)

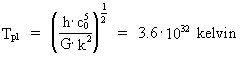
In (10), k = 1.38·10^-23 J/K is Boltzmann's constant, which is a coupling parameter between the energy of a system and its equivalent absolute temperature.

The context between the cosmological elementary units and the Planck units
We get a context between the Planck units and the units discovered by me by writing the ratio between the Planck length l_pl and the elementary length r₀. We get:

(11)

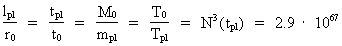
where N³(t_pl) is the value of the cosmic evolution quantum number, when the Universe had an extension equal to the Planck length and an age equal to the Planck time. This number – which is a natural number – also gives the number of matter/energy quanta – unitons – in the Universe, when its age was Planck time!
T₀ = 10.4 · 10⁹⁹ kelvin is the formal energy equivalent absolute 'particle temperature' when the Universe was 'born'. As the temperature value is a statistically defined quantity, related to a system containing a great amount of particles, T₀ is a purely formal quantity, as the Universe only consisted of one quantum – the cosmic embryoton – when it was 'born'.
Comparing with the cosmological basic equation (5) we see the following:
The Planck mass is equal to the mass of a uniton, when the Universe had the age equal to Planck time!
When the Universe had an extension equal to the Planck length 4.0·10^-35 m, with an age equal to Planck time 1.3·10^-43 s, it consisted of 2.9·10⁶⁷ unitons, each with a mass equal to the Planck mass 5.5·10^-8 kg!   The equivalent absolute temperature of the Universe, T_pl, was in this state 3.6·10³² kelvin and can be calculated by:

(12)

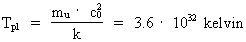
where m_u = 5.5 · 10^-8 kg = m_pl

which is identical to the value in equation (10).

The gravitational 'constant' when the Universe had an age equal to Planck time
From my holistic quantum cosmology it follows that gravitation in the Universe is constantly decreasing. The context between Newton's gravitational 'constant', G, at an age, T, of the Universe, and its value G₀, when the Universe was 'born' is given by:

(13)

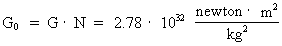
From (13) we can calculate the value of G when the Universe had an age equal to Planck time, and we get:

(14)

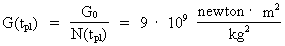
thus about 10²⁰ times higher than in our epoch. This value is equal to Coulomb's constant. Whether this is accidental is worth a consideration.

From the above we see that the Planck quantities are 'just' some connected values for physical quantities, characterizing the Universe when it had an extension equal to the Planck length. The Planck quantities can be deducted from the most fundamental physical quantities in the Universe:
Elementary length, elementary time and the total matter/energy mass of the Universe!

© Louis Nielsen, 29.november 1997
E-mail: louis44nielsen@gmail.com

  Next article