|
By Louis Nielsen, Herlufsholm
In 1998 were made some new cosmological observations which by the
American magazine Science were announced as
"Breakthrough of the Year" (Science, December
18, 1998), The discovery was that the Universe apparently has an
accelerating expansion. Scientific American, in its January 1999
issue, calls the discovery a cosmological revolution. One of the
conclusions is a.o. that the Universe will continue its expansion and
not - as assumed by many cosmological models - eventually change it
into a contraction. The calculations made are a.o. based on spectrum
analyses and measurements of luminosity of distant supernovae of the
type Ia.
The conclusions of the respective teams are that supernovae, belonging
to distant galaxies, are situated at distances which are greater
than what would be expected according to current cosmological
models. This must mean that the galaxies in question have moved faster
than expected and thereby obtained a higher acceleration than what had
hitherto been believed, according to these models. To save the
traditional cosmological models the teams now try to introduce
'patching' solutions, supported by new and old effects, such as 'dark
energy' and the re-introduction of the 'cosmological constant' in
Einstein's general field equations, etc. The discovery, that distant
galaxies move with a higher speed than expected by the traditional
cosmological theories, is a support to my quantum theory about the
Universe, – based on quantization of distance, time interval and
mass. The new observations of the expansion of the Universe can be
explained by my theory.
The Hubble relation and the disagreement on the value of
the Hubble constant In the traditional and established cosmology, which is based on Einstein's general theory of relativity from 1915, it is attempted to determine the numerical value of some parameters in the equations, so that a given cosmological model approaches the observations made in the real Universe. A very important quantity in these traditional, parametrized cosmological theories is the so called Hubble constant, H. It enters as a proportionality constant in the famous Hubble relation, which gives the connection between f.i. the relative radial speeds, vr, of two galaxies, and the distance, d, between the galaxies. The Hubble relation is given by: (1) 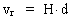 The Hubble relation is named after Edwin Powell Hubble (1889-1953). He discovered in 1929, that – for the stars of most galaxies – there is a systematical shift of the wavelength of the different colors towards the red part of the spectra of the stars, viz. towards longer wavelength. Hubble discovered that the relative shift of wavelength is proportional to the distance, d, between the observer and the emitting object. This discovery was quickly interpreted as a Doppler effect (discovered 1842 by Christian Doppler (1803-1853)), caused by the relative velocity of the emitting object and the observer. That the wavelengths are shifted towards red show that the emitting objects are moving away from the observer, and this is interpreted as an expansion of the Universe. The classical Doppler equation can be written: (2) 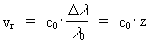
where (3) 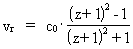
By measuring the relative shift of wavelength, z, of a specific
spectral line, found in the light from a star in a galaxy, you can, by
using (3) or (2) together with (1), determine the distance, d, to a
galaxy, on the condition that you know the value of H. There is,
however, considerable disagreement on this value, which the following
will show. There has been – and still is – strong disagreement on the value of the Hubble constant, H. Different researchers have obtained the following values:
H1 = 83±13 km/s/Mpc =
(2.68±0.42)·10-18 s-1 , (Madore.
Science, vol. 255, p. 405, (1992))
The most cited value for the Hubble constant is H = 80±17
km/s/Mpc. Radial velocities, calculated by means of respectively the Hubble relation and my expansion equation In chapter (2) of my 'Holistic Quantum Cosmology with Decreasing Gravity' I derive the following cosmologically general expansion formula, valid for two mass systems, moving away from each other due to the decreasing gravity: (4) 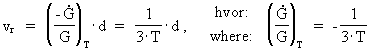
(5) 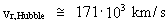
In order to be able to calculate the radial velocity according to my
equation (4) we first need to calculate the value of (6)  We can now calculate the radial velocity by means of my expansion formula (4). We get: (7) 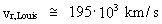 The relative procentual difference between the values in (5) and (7) is about 14%, viz. my calculated value is about 14% higher than what would be expected by using the Hubble relation. If H1 is used in the Hubble relation, you get a relative procentual difference of about 10%, and if H2 is used, then about 12%.
Conclusion
Louis Nielsen, January 1999
|
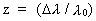 and
c0 is the velocity of light,
and
c0 is the velocity of light, 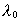 the measured wavelength in the laboratory of a specific
spectral line,
and
the measured wavelength in the laboratory of a specific
spectral line,
and 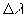 the difference between the measured wavelength and the measured wavelength
in the loboratory.
At greater velocities
(about 1% of the velocity of light) it is necessary to use the
relativistic Doppler equation, given by:
the difference between the measured wavelength and the measured wavelength
in the loboratory.
At greater velocities
(about 1% of the velocity of light) it is necessary to use the
relativistic Doppler equation, given by:
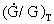 is equal to the relative
derivative of G with respect to time and is dependent on an actual
age, T, of the
Universe. (· denotes the first derivative with respect to time).
vr is the instantanouos value of the radial velocity of a
light emitting object, relative to an observer, when light was emitted
from that object, and corresponding to a
retarded age of the Universe, T1, which is lower than the
actual age of the Universe. d is the distance which the
light travels in the time interval from it was emitted and until it is
received – for instance by us as observers.
is equal to the relative
derivative of G with respect to time and is dependent on an actual
age, T, of the
Universe. (· denotes the first derivative with respect to time).
vr is the instantanouos value of the radial velocity of a
light emitting object, relative to an observer, when light was emitted
from that object, and corresponding to a
retarded age of the Universe, T1, which is lower than the
actual age of the Universe. d is the distance which the
light travels in the time interval from it was emitted and until it is
received – for instance by us as observers.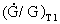 , when the Universe was T1
years old. We get:
, when the Universe was T1
years old. We get: