Universets masse, udstrækning og alder
kombineret med naturkonstanter
Omnia determinant
omnia
![]()
Af Louis Nielsen
cand.scient. i fysik og astronomi
Lektor ved Herlufsholm
louis44nielsen@gmail.com
Forening af
Makrofysik og Mikrofysik
Eksisterer der matematisk-fysiske sammenhænge mellem fysiske størrelser, der er karakteristiske for Universet som helhed, og størrelser der er karakteristiske for atomare partikler?
Med andre ord: Eksisterer der en sammenhæng mellem naturkonstanterne, der er karakteristiske for makrofysik og mikrofysik?
I det følgende vises, at ovenstående spørgsmål kan besvares med: Ja!
Det vises, at der gælder matematisk-fysiske sammenhænge mellem Universets totale masse, dets udstrækning og alder og kendte naturkonstanter, såsom Newtons gravitationskonstant, lysets hastighed, Plancks konstant og masserne af elektronen og protonen og deres geometriske udstrækninger.
Sammenhæng næppe en
tilfældighed
Hvis man udregner brøkforholdet mellem massetætheden (dvs.
masse pr. rumfangsenhed) af en elektron og den gennemsnitlige massetæthed af
Universet, så får man et tal uden enhed af størrelsesordenen![]() . Dette tal er så tæt på talværdien
. Dette tal er så tæt på talværdien![]() , der angiver styrkeforholdet mellem de elektriske kræfter og
de gravitationelle kræfter mellem to elektroner, at man må formode, at det er
dette brøkforhold der er tale om.
, der angiver styrkeforholdet mellem de elektriske kræfter og
de gravitationelle kræfter mellem to elektroner, at man må formode, at det er
dette brøkforhold der er tale om.
Hvis man udregner brøkforholdet mellem massetætheden af en
proton og den gennemsnitlige massetæthed af Universet, så får man et tal uden
enhed af størrelsesordenen![]() . Dette tal er så tæt på talværdien
. Dette tal er så tæt på talværdien![]() , der angiver styrkeforholdet mellem de elektriske kræfter og
de gravitationelle kræfter mellem to protoner, at der også her må antages at
gælde lighed.
, der angiver styrkeforholdet mellem de elektriske kræfter og
de gravitationelle kræfter mellem to protoner, at der også her må antages at
gælde lighed.
Massetæthederne af
protonen, elektronen og Universet
Det må antages, at der gælder følgende meget interessante sammenhænge mellem de gennemsnitlige massetætheder af henholdsvis protonen, elektronen og Universet som helhed:
(1) 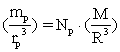
(2) ![]()
I ligning (1) er ![]() hvilemassen af en
proton og
hvilemassen af en
proton og![]() er protonens gennemsnitlige radius (eller diameter).
Protonens radius er målt til
er protonens gennemsnitlige radius (eller diameter).
Protonens radius er målt til![]() .
.
I ligning (2) er ![]() hvilemassen af en elektron og
hvilemassen af en elektron og ![]() er elektronens
gennemsnitlige radius (eller diameter).
er elektronens
gennemsnitlige radius (eller diameter).
M er den totale masse af Universet og R dets gennemsnitlige udstrækning (radius).
![]() er lig med
brøkforholdet mellem størrelserne af de elektriske kræfter
er lig med
brøkforholdet mellem størrelserne af de elektriske kræfter![]() og de gravitationelle kræfter
og de gravitationelle kræfter![]() mellem to protoner.
mellem to protoner.
![]() er lig med brøkforholdet
mellem størrelserne af de elektriske kræfter
er lig med brøkforholdet
mellem størrelserne af de elektriske kræfter![]() og de gravitationelle kræfter
og de gravitationelle kræfter![]() mellem to elektroner.
mellem to elektroner.
![]() og
og ![]() er defineret ved
følgende
er defineret ved
følgende
(3) 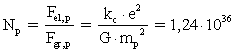
(4) 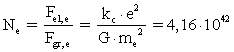
I ligningerne (3) og (4) er ![]() Coulombs konstant og
Coulombs konstant og ![]() er den numeriske elektriske ladning af en elektron og en
proton.
er den numeriske elektriske ladning af en elektron og en
proton.
Størrelsen![]() er Newtons gravitationskonstant i vor epoke.
er Newtons gravitationskonstant i vor epoke.
Af ligningerne (1) og (2) ser vi, at massetætheden af en
proton og en elektron er ligefrem proportional med Universets aktuelle
gennemsnitlige massetæthed. Proportionalitetskonstanterne![]() og
og ![]() angiver
styrkeforholdet mellem de elektriske kræfter og de gravitationelle kræfter
mellem henholdsvis to protoner og to elektroner.
angiver
styrkeforholdet mellem de elektriske kræfter og de gravitationelle kræfter
mellem henholdsvis to protoner og to elektroner.
Universets masse
beregnet ved hjælp af atomfysiske konstanter
Fra ligning (1) kan vi isolere Universets masse M:
(5) 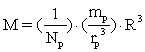
Universets udstrækning R er vurderet til at være af
størrelsesordenen![]() . Med denne talværdi for R fås:
. Med denne talværdi for R fås: ![]()
Ifølge undertegnedes kvantekosmologi (se link) postuleres følgende
sammenhæng at gælde:![]()
(6) ![]()
I ligning (6) er ![]() Plancks konstant og
Plancks konstant og ![]() er lysets hastighed.
er lysets hastighed.
Ved kombination af ligningerne (5) og (6) (og lidt regning) kan Universets totale masse M udtrykkes ved følgende atomfysiske størrelser:
(7) 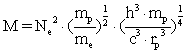
Ligning (7) giver en kosmologisk fundamental sammenhæng mellem Universets totale masse M og kendte naturkonstanter, såsom massen af elektronen og dennes elektriske ladning, massen af protonen og dennes radius, Coulombs konstant, Plancks konstant, Newtons gravitationskonstant og lysets hastighed.
Da de to første faktorer i udtrykket (7) er ubenævnte størrelser (rene tal), så angiver sidste faktor en masse.
Den eneste størrelse på højre side af ligning (7) som er
målt med nogen usikkerhed er protonens udstrækning![]() . Men som nævnt er den cirka
. Men som nævnt er den cirka ![]() . Hvis denne værdi benyttes i formel (7), så bliver sidste
faktor i udtrykket meget tæt på hvilemassen af en proton, og
. Hvis denne værdi benyttes i formel (7), så bliver sidste
faktor i udtrykket meget tæt på hvilemassen af en proton, og![]() vil da være identisk med den såkaldte Compton-bølgelængde.
vil da være identisk med den såkaldte Compton-bølgelængde.
Universets masse
Talværdien af Universets totale masse M kan beregnes af formel (7). Vi får:
(8) ![]()
Universets
udstrækning
Af ligning (6) kan vi beregne Universets udstrækning R:
(9) ![]()
Talværdien af R i (9) er i overensstemmelse med beregninger foretaget i andre kosmologiske modeller af Universet.
Den Kosmiske
Embryoton. Det Embryonale Koordinat-system
Universet begyndte sin dynamiske kvante-udvikling med alt stof
og energi koncentreret i en uhyre lille ’partikel’ som vi kan kalde den Kosmiske
Embryoton, en betegnelse for den foster-tilstand, hvor alt stof og energi var
koncentreret inden for en udstrækning, der definerer den fysisk mindste afstand,
afstands-kvantet![]() givet ved:
givet ved:
(10) ![]()
Universets kvante-udvikling er forgået ved successive delinger af den oprindelige Kosmiske Embryoton. De dannede stof-/energi-kvanter har siden ved forskellige typer rekombinationer dannet alle de ’partikler’ der eksisterer i det aktuelle Univers.
Den Kosmiske Embryoton kan definere et abstrakt matematisk embryonalt reference-system med et absolut centrum for det udviklende Univers. Positioner og bevægelsesforhold for alle dannede stof-/energi kvanter kan, i princippet, henføres og beregnes i forhold til det embryonale kosmologiske koordinatsystem, Embryoton-systemet.
Invariant og absolut
hastighed c
Den kosmiske embryotons første kvante-delings proces dannede
stof-/energi-kvanter, der bevægede sig af sted med hastigheden c, målt i
forhold til det Embryonale koordinatsystem. Hastigheden c, der er lig med den
kendte hastighed af lys, er bestemt af brøk-forholdet mellem afstands-kvantet ![]() og tids-kvantet
og tids-kvantet ![]() . Dvs. der gælder:
. Dvs. der gælder:
(11)![]()
![]()
Da både![]() og
og ![]() er absolutte og
invariante størrelser, så gælder dette også hastigheden c, dette helt i
overensstemmelse med målinger af lysets hastighed, der viser at det er en
absolut, ikke-relaviv, størrelse. Forklaringen på denne ikke-relative hastighed
af c er således forklaret i ligning (11).
er absolutte og
invariante størrelser, så gælder dette også hastigheden c, dette helt i
overensstemmelse med målinger af lysets hastighed, der viser at det er en
absolut, ikke-relaviv, størrelse. Forklaringen på denne ikke-relative hastighed
af c er således forklaret i ligning (11).
Universets alder
De efterhånden dannede stof-/energi-kvanter har med farten c og indtil vor epoke tilbagelagt en strækning lig med Universets aktuelle ’radius’ R.
Universets alder T siden dets ’fødsel’ kan således beregnes af:
(12) ![]()
Den her, meget simpelt, beregnede værdi af Universets alder er, ganske interessant, lig med den alder der (for tiden) regnes med i den etablerede kosmologi!
Tids-kvantet eller tids-atomet
Ved benyttelse af ligning (6) kan Universets alder T skrives:
(13) ![]()
’Tiden-forløbet’![]() angiver det mindste fysiske tidsinterval, tids-kvantet eller
tidsatomet, givet ved:
angiver det mindste fysiske tidsinterval, tids-kvantet eller
tidsatomet, givet ved:
(14) ![]()
Elektronens
udstrækning
Af ligning (2) kan vi beregne elektronens udstrækning![]() :
:
(15) 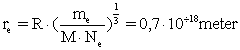
Målinger af elektronens udstrækning er stadig usikre, men de giver en værdi, der er af størrelsesordenen som teoretisk beregnet i ligning (15).
Holisme-princippet.
Omnia determinant omnia. Evolution af Naturlovene
I øvrigt: Det er den totale stof og energimængde i Universet, der er den afgørende og mest fundamentale fysiske størrelse. Vi kan kalde det ’Holisme-princippet’ eller ’Det Holistiske Princip’.
Størrelsen af Universets totale masse er bestemmende for talværdierne af naturkonstanterne, hvoraf nogle af dem varierer efterhånden som Universet udvikler sig.
Naturlovene er også underlagt kosmisk evolution.
’Omnia determinant omnia’. ’Alt bestemmer alt’.
Louis Nielsen
21/6-2008