Louis Nielsen
Holistisk kvantekosmologi
med
aftagende gravitation
2. del
Ny teori om universet
Conditio embryonis omnia determinat
Afhandling
© Copyright 1996 Louis Nielsen
2. del
Fysiske konsekvenser af en aftagende gravitation
Af Louis Nielsen
Da der virker en tiltrækkende tyngdekraft mellem alle massedele i universet, vil en
stadigt aftagende gravitation
bevirke en stadigt større og større afstand mellem disse. Konsekvensen er, at
alt udvider sig!
En stadigt aftagende gravitation i vort univers medfører flere fysiske
konsekvenser, som vil kunne
påvises mere eller mindre let. Vi vil i det følgende analysere nogle af de
forhold i universet, der er
afhængige af gravitationens størrelse.
Hvis vi går tilbage til et yngre og yngre univers, går vi tilbage til epoker,
hvor gravitationen var
større og større. Men hvordan kan vi få viden om begivenheder, der
fandt sted for måske
milliarder af år siden? Jo, ved at observere objekter, der befinder sig længere og
længere borte fra os!
Da vi får informationerne i fortrinsvis det lys, objekterne udsender, og dette lys
bevæger sig med en
endelig hastighed, ja da »ser« vi tilstanden af objektet, som den var på det
tidspunkt, da lyset blev
udsendt fra det.
Nogle af de objekter, der menes at befinde sig længst væk og som
sådan giver de ældste
informationer, er de såkaldte quasarer. Disse objekter viser sig at udstråle
kolossale energimængder
fra et relativt lille geometrisk område. Og dette er en aktuel »gåde«
for astronomer og
fysikere. En universel aftagende gravitation kan måske give en forklaring.
En geofysisk effekt af en aftagende gravitation er, at jordkloden »pustes«
op, dvs. dens radius
vokser med tiden. Dette bevirker dels, at den faste jordskorpe revner, og dette kan forklare
den såkaldte
kontinentaldrift, det fænomen, at kontinenterne bevæger sig fra hinanden. Dels
bevirker jordens
»oppustning«, jorden roterer langsommere og langsommere omkring sig selv,
dvs. at jorddøgnet
bliver længere og længere! Tidligere i jordens udviklingshistorie bevægede
den sig meget hurtigere.
Ved at studere kontinentaldrift og fossiler kan man få vidnesbyrd om en aftagende
gravitation. Det sidste skyldes
det forhold, at visse koraller udvikler et kalklag for hvert døgn, og
undersøgelser har vist, at koraller, der
er millioner af år gamle, har tyndere og flere kalklag, end hvad der er tilfældet i
vor tid.
Planetfysisk betragtet vil en aftagende gravitation bevirke: At månen fjerner sig
fra jorden, og alle
afstandene i vort solsystem forøges. Af formlerne kan det beregnes, at jordens radius
vokser med omkring
0,02 centimeter pr. år, svarende til at jordens radius er vokset omkring 100 kilometer i
løbet af de sidste
500 millioner år! Denne »oppustning« af jorden kan forklare de
kræfter, der har revnet
jordskorpen og bevirket en adskillelse af kontinenterne!
Som følge af en aftagende tyngdekraft forøges afstanden mellem jorden
og månen med
omkring 1,2 centimeter pr. år.
Ved jordens forøgelse fjernes dens masse længere og længere fra
omdrejningsaksen, og dette
bevirker, at jordens rotationshastighed bliver mindre og mindre (sammenlign med en
skøjteløber, der
strækker armene ud fra kroppen for at mindske sin rotationshastighed!). Jordens lavere
rotationshastighed er
ensbetydende med, at jorddøgnet forlænges. Det er ganske vist små
størrelser, der er tale
om, så det kan kun konstateres over lange tidsrum. I løbet af de sidste 500
millioner år er
døgnet blevet forlænget med omkring 1 time som følge af jordens
»oppustning«. En
anden effekt, der dog også har givet en yderligere forøgelse af døgnet,
er det, man kalder
tidevands- og tidejordskræfter, altså det fænomen, der giver høj- og
lavvande. Dette skyldes
specielt månens, men også solens tyngdekrafttræk på jorden. Disse
kraftvirkninger bevirker en
langsom opbremsning af jorden!
Alt ekspanderer som følge af en aftagende gravitation
I det følgende vil vi udlede en formel, der giver en sammenhæng mellem den
rumlige ekspansion af et
graviterende system og den relative aftagen af gravitations-»konstanten«.
Formlen kan vi kalde den
generelle ekspansionsformel.
Lad os betragte en partikel med den gravitationelle masse m1,
der bevæger sig i en cirkelbane -
der vil ekspandere - omkring en anden graviterende partikel med massen
m2. Bevægelsen af
m1 er bestemt ved Newtons 2. lov og gravitationsloven med den til
enhver tid gældende talværdi
af gravitations-»konstanten«. Der gælder:
(1) 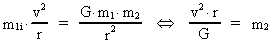
hvor v er hastigheden af m1, og r er den
øjeblikkelige afstand mellem
m1 og m2.
m1i angiver den inertielle masse af den omkredsende partikel. Vi vil
betragte hastigheder, der er relativt
små i forhold til lyshastigheden og vil derfor antage lighed mellem den inertielle
masse og den gravitationelle
masse, m1i = m1.
I stedet for Newtons notation, hvor en prik over et bogstav betyder differentiation med
hensyn til tiden, må vi af praktiske grunde i nogle tilfælde her sætte et
efterstillet ´ (f.eks. v´). Af ligning (1) får vi:
(2) 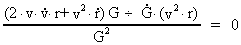
Dette udtryk kan yderligere omformes til:
(3) 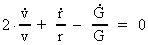
Da der er tale om en centralkraft, gælder der
impulsmomentbevarelse, dvs. der gælder:
(4) 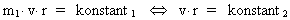
Af ligning (4) fås:
(5) 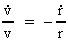
Dette udtryk indsat i (3) giver for den relative forøgelse af r
følgende udtryk:
(6) 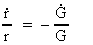
(Ekspansionsformlen)
For den relative variation af hastigheden har vi følgende udtryk:
(7) 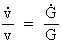
Ligning (6) angiver den radiale hastighed, hvormed to graviterende masser i
afstanden r ekspanderer fra
hinanden. Relationen er en teoretisk udledning af den kosmologiske
Hubblerelation!
Vi vil benytte (6) til at beregne den tidslige forøgelse af jordens
radius og dens tidslige forøgelse af
afstanden til månen, idet vi vil antage, at
(8) 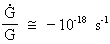
og at denne værdi er nogenlunde konstant i vor epoke.
For jordradiens forøgelse får vi med r = 6400 km:
(9) 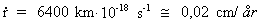
Benyttes ligning (6) på jord-måne-systemet, beregnes en tidslig
afstandsforøgelse af
størrelsen: r = 384,4 · 10³ km.
(10) 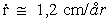
Laserlysforsøg viser, at afstanden til månen forøges med ca. 5
cm/år. Resultatet i (10)
giver kun det bidrag, der skyldes en aftagende gravitation. Resten skyldes andre
gravitationelle virkninger, såsom
»tide«-kræfter.
Palæomagnetiske analyser har vurderet en øvre grænse
på 0,13 mm/år for Jordens
radiusforøgelse, i god overensstemmelse med talværdien i (9).
Talværdien i (9) afhænger af
nøjagtigheden i bestemmelsen af
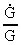 . .
(Reference: Mcelhinny et al. Nature, 271, 316-321, (1978)).
Jordens ekspansion og jorddøgnets forlængelse.
Kontinentaldrift
Efterhånden som gravitationen aftager, vil jorden - og alle andre kloder -
»puste« sig op med det
resultat, at massen bliver fordelt længere og længere fra omdrejningsaksen. Dette
bevirker, at
rotationshastigheden bliver mindre og mindre (sammenlign med skøjteprinsessen, der
strækker armene ud
for at mindske sin rotationshastighed). En lavere rotationshastighed er ensbetydende med, at
jorddøgnet bliver
længere. Jorden bremses langsomt op! Med fagtekniske ord forøges jordens
inertimoment,
efterhånden som dens radius vokser.
I det følgende vil jeg udlede en formel, der giver en sammenhæng mellem
jordens rotationstid
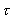 omkring sig selv til et bestemt
tidspunkt og den til dette tidspunkt hørende gravitations-
»konstant«. Da gravitations-»konstantens« størrelse
afhænger af universets
aktuelle alder, gives også en direkte sammenhæng med denne. omkring sig selv til et bestemt
tidspunkt og den til dette tidspunkt hørende gravitations-
»konstant«. Da gravitations-»konstantens« størrelse
afhænger af universets
aktuelle alder, gives også en direkte sammenhæng med denne.
Jordens impulsmoment Lj kan udtrykkes ved dets inertimoment med
hensyn til omdrejningsaksen og
vinkelhastigheden sådan:
(11) 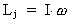
Hvor I er inertimomentet, og
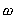 er vinkelhastigheden. Idet vi
antager, at impulsmomentet
holder sig konstant ved »oppustningen«, gælder der: er vinkelhastigheden. Idet vi
antager, at impulsmomentet
holder sig konstant ved »oppustningen«, gælder der:
(12) 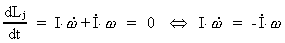
Inertimomentet af en kugle er givet ved:
(13) 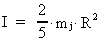
hvor mj er jordens masse og R dens øjeblikkelige
radius.
Differentiation af I med hensyn til tiden giver:
(14) 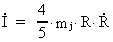
Idet der gælder:
(15) 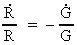
får vi ved sammenkobling af formlerne:
(16) 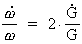
Denne ligning integreres, og idet t1 og t2, hvor
t2 > t1, er to tidspunkter, får
man:
(17) 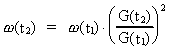
Idet sammenhængen mellem
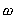 og rotationstiden og rotationstiden
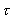 er givet ved: er givet ved:
(18) 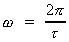
kan vi udlede følgende udtryk:
(19) 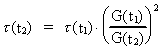
Den aktuelle talværdi af gravitations-»konstanten« afhænger af
universets aktuelle alder. Denne
sammenhæng er bestemt ved formlen:
(20) 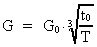
hvor G0 er universets initielle gravitations-»konstant«, og
t0 er elementartiden.
Benyttes dette udtryk for gravitations-»konstanten« G i udtrykket for
rotationstiden, får vi
følgende formelsammenhæng:
(21) 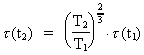
Denne formel kunne i øvrigt være udledt direkte ud fra
impulsmomentbevarelse. Vi vil beregne et par
taleksempler. Først vil vi beregne den rotationstid
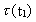 , som jorden
havde i devontiden for ca. 400 millioner år siden. Idet vi
benytter talværdierne: , som jorden
havde i devontiden for ca. 400 millioner år siden. Idet vi
benytter talværdierne:
T2 = 10,5 · 109 år;
T1 = 10,1
· 109 år;
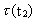 = 24 h
får vi: = 24 h
får vi:
(22) 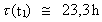
Analyser af koraller fra devontiden viser, at de havde flere og tyndere kalklag, end de samme
koralarter har i vor
epoke. Idet hvert kalklag svarer til et jorddøgn, har man udregnet (med megen
usikkerhed), at jorddøgnet
var på ca. 22 timer. Da jorddøgnets længde også bestemmes
specielt af månens
tyngdekrafttræk i den faste og flydende jordskorpe med opbremsning til følge,
passer ovennævnte
beregning ganske godt, idet en mindre talværdi end 24 timer skulle have været
benyttet.
Jordens »oppustning« som følge af en aftagende gravitation kan give en
dynamisk forklaring
på kontinentaldriften, den effekt at kontinenterne langsomt driver fra hinanden. I
løbet af de sidste 500
millioner år er jordens radius forøget med omkring 100 km, hvilket har givet
anledning til enorme
revnedannelser i kontinenterne og drevet dem fra hinanden, i øvrigt også
hjulpet til af
centrifugalkraften.
Visse forskere har analyseret den relative tidslige aftagen af jordens
vinkelhastighed 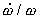 .
Den observerede værdi er angivet til: .
Den observerede værdi er angivet til:
(16a) 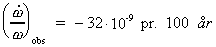
En relativt stor effekt er bestemt af de gravitationelle »tide«-kræfter fra
specielt månen og
solen. Denne effekt bidrager med en talværdi af størrelsen:
(16b) 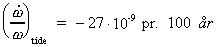
altså ikke nok til at forklare den observerede værdi!
Men hertil kommer så et bidrag fra den aftagende gravitation. Dette bidrag kan
udregnes af formel (16), og vi
får:
(16c) 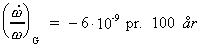
Kombineres disse to bidrag, får vi:
(16d) 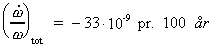
altså en ganske god overensstemmelse med den observerede værdi!
Aftagende gravitation og masse - lysstyrkerelationen for stjerner
Energiudstrålingen fra en stjerne (eller en galakse) viser sig at være meget
afhængig af stjernens
masse m og gravitations-»konstanten« G. Det kan vises, at
der gælder
følgende sammenhæng mellem den energiudstrålende effekt P
og m og
G. Relationen kaldes som regel for masse-luminositetsrelationen:
(23) 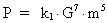
k1 er en systemafhængig proportionalitetskonstant. Relationen
er uafhængig af specifikke
energiproducerende processer.
Lad os beregne forholdet mellem energiudstrålingen til to forskellige tidspunkter
svarende til to forskellige
talværdier af gravitations-»konstanten«, dvs. til to forskellige aldre
T1 og T2 af
universet. Vi kan således opskrive brøkforholdet:
(24) 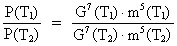
Hvis massen antages at være ens til de to tidspunkter, dvs. m(T2) =
m(T1), da har vi:
(25) 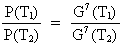
Indsættes udtrykket for G's aftagen med universets alder, fås:
(26) 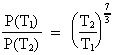
Af ligning (26) ser vi, at energiudstrålingen af et objekt, der befinder sig langt fra os -
eksempelvis en quasar -
er meget større, idet lyset fra dette objekt blev sendt af sted på et tidspunkt,
hvor gravitations-
»konstanten« var større, svarende til en lavere alder af universet.
Som taleksempel kan vi tage: T1 = 0,5 · 109
år & T2 = 10,5 · 109
år. Dette giver:
(27) 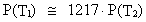
Det gælder også, at massefordelingens udstrækning afhænger af
G, således at
denne var koncentreret inden for et mindre område i tidligere epoker.
Der gælder nemlig følgende relation:
(28) 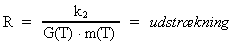
For to universaldre gælder da:
(29) 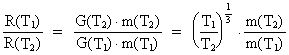
Med de samme aldre som ovenfor får vi for udstrækningen i en tidligere
epoke:
(30) 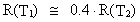
Hvis vi i formlerne (26) og (29) benytter talværdierne T1 =
106 år og
T2 = 10,5 · 109 år, får vi for
henholdsvis energiudstrålingen og objektets
udstrækning følgende værdier svarende til universalderen
T1 = 106 år:
(31) 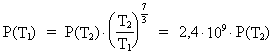
(32) 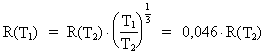
Vi ser af udtrykkene (31) og (32), at desto længere borte og dvs. desto yngre objekter,
vi observerer, desto
større energiudstråling og desto mindre udstrækning har
disse objekter. Disse forhold
er netop gældende for de såkaldte quasarer, nemlig at de udstråler enorme
energimængder fra
et relativt lille område. Quasarerne vides også at befinde sig i de yderste dele af
vort univers, dvs. vi
observerer objekter, der er meget »unge«. Den ovenfor givne redegørelse
kan således
være løsningen på quasarproblemet!
I øvrigt har nyere fotograferinger med meget lang eksponeringstid vist, at quasaren
sandsynligvis blot er det
centrale område - galaksekernen - af en meget fjern galakse, der har mange ligheder
med de såkaldte N-
galakser (N for nucleus), der befinder sig nærmere os, og de såkaldte
Seyfert-galakser, der er endnu
nærmere os. Disse tre galakse-»typer«, S-, N- og Q-galakser, kan vise sig
at være vidnesbyrd
om en kosmisk aftagende gravitation.
Af udtrykkene i (23) og (28) kan vi bestemme den relative tidslige variation af P og
R. Vi får:
(33) 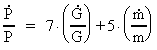
og
(34) 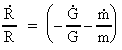
Da 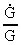 og og
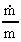 er aftagende funktioner med tiden,
ser man, at er aftagende funktioner med tiden,
ser man, at 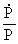 aftager med tiden,
og aftager med tiden,
og 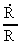 vokser med
tiden. vokser med
tiden.
Efterskrift
Den her fremlagte teori giver løsningen på de store tals 'mysterium',
idet N spiller
rollen som en kosmisk evolutionsoperator, hvis talværdi ved universets fødsel
var lig med 1.
Teorien er i overensstemmelse med Machs princip, idet den sammenkobler mikro- og
makrokosmos!
Teorien giver også et svar på 'eksistensen af en tidens pil', dvs. det faktum, at
tiden kun går i en
retning. Dette er opfyldt i og med, at det kosmiske rumkvantetal og dermed det kosmiske
tidskvantetal springer fra
tallet 1 og op igennem større og større tal.
Centrifugal- og corioliskraftens identitet med
N¯-felt-kraften
Siden mekanikkens tidligste barndom er der blevet filosoferet over de
såkaldte fiktive kræfter, også kaldet systemkræfter,
idet de kun gav sig til kende i accelererede systemer. Eksempler
på disse systemkræfter er: Centrifugalkræfter og
corioliskræfter. Det spørgsmål, der kan stilles,
er: Er disse kræfter virkelige fiktive, eller er de relle fysiske
kræfter, der forårsages af andre fysiske
systemer? Spørgsmålet er specielt taget op af Isaac Newton
(1642-1727), George Berkeley (1685-1753), Ernst Mach (1838-1916) og
Albert Einstein (1879-1955). Problemstillingen kan illustreres
som følger:
Betragt en kugle, der roterer i forhold til resten af universets masser.
Erfaringen siger, at kuglen vil bule ud ved de ækvatoriale
områder. Spørgsmålet er: Hvorfor buler kuglen ud?
Newton svarede: Kuglen buler ud, fordi den roterer i forhold til det
absolutte rum. Er kuglen i hvile i forhold til det
absolutte rum, vil den ikke bule ud, svarede Newton. Mach derimod sagde,
at der er tale om en relativ effekt, der lige
så vel ville
opstå, hvis det var hele universet, der roterede i forhold til kuglen. Newton og Mach
var således ikke
enige. Einstein gik ind for Machs opfattelse - alt er relativt - og søgte at inkorporere
dette såkaldte Machs
princip i sine relativitetsteorier.
Machs princip kan formuleres således:
De lokale fysiske virkninger er bestemt relativt af det resterende univers'
tilstand.
Jeg er enig i Machs opfattelse, idet jeg vil formulere det helt generelt:
Alt er bestemt af alt! - Omnia determinant omnia.
I det følgende vil vi undersøge identiteten mellem
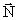 -felt-kraften og centrifugal- og
corioliskraften. -felt-kraften og centrifugal- og
corioliskraften.
Den universelle
N¯-felt-krafts identitet med
centrifugalkraften
I et inertialsystem betragtes en partikel med den gravitationelle masse
mg. Lad denne rotere i en cirkelbane
med radiusvektor
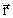 og vinkelhastighed og vinkelhastighed
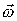 . Centrifugalkraftvektoren er
da givet ved: . Centrifugalkraftvektoren er
da givet ved:
(1a) 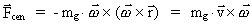
Vi ser, at den matematiske form er fuldstændig identisk med
formeludtrykket for den gravitationelle
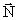 -felt-kraft, der er givet ved: -felt-kraft, der er givet ved:
(2a) 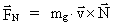
(Fra ligning (9.6))
I formlerne er  den gravitationelle
masses hastighed i den gravitationelle
masses hastighed i 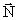 -feltet. -feltet.
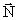 -feltets størrelse og retning
er således identisk med -feltets størrelse og retning
er således identisk med
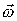 . .
Da de samlede masser i universet relativt set roterer i modsat retning
af den roterende partikel, forårsager det et
induceret 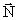 -felt i det område, hvor
partiklen roterer. Det nøjagtige formeludtryk til
beregning af -feltets størrelse
afhænger af den geometriske massefordeling omkring den
roterende partikel. Hvis vi antager, at den -felt i det område, hvor
partiklen roterer. Det nøjagtige formeludtryk til
beregning af -feltets størrelse
afhænger af den geometriske massefordeling omkring den
roterende partikel. Hvis vi antager, at den
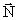 -feltinducerede gravitationelle masse
Mg
fordeles i en massering med radius R, fås et formeludtryk af
formen: -feltinducerede gravitationelle masse
Mg
fordeles i en massering med radius R, fås et formeludtryk af
formen:
(3a) 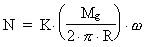
(Fra ligning (9.4))
hvor K er den dynamiske koblingskonstant til
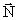 -feltet. Idet vi sætter N = -feltet. Idet vi sætter N =
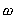 , fås for
masse-afstandsforholdet: , fås for
masse-afstandsforholdet:
(4a) 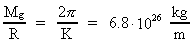
En nærmere analyse, hvor der tages hensyn til feltets endelige
udbredelseshastighed, K's variation og en
nøjagtigere geometri, vil bekræfte ovenstående.
Inerti - et mål for gravitationelle kraftvirkninger
En partikel »udviser« inerti (træghed, modstand), hvis den skal have
ændret sin hastighed -
målt i forhold til et inertialsystem - dvs. hvis den skal accelereres. Denne
inertiegenskab er indført i
Newtons 2. lov som partiklens inertielle masse mi.
mi spiller rollen som proportionalitetsfaktor mellem partiklens
acceleration og den resulterende virkende kraft
på partiklen. Newtons 2. lov lyder da:
(5a) 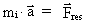
hvor 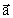 er accelerationen og er accelerationen og
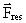 den resulterende kraft. den resulterende kraft.
Man kan nu spørge: Hvad forårsager denne inerti, der virker
som en kraft modsat rettet den kraft, man påvirker partiklen med?
Et nærliggende svar er: Der er tale om en gravitationel selvinduktion
forårsaget af den relative
bevægelse i forhold til resten af masserne i universet!
Hvis ovenstående svar er reel sandhed, er det nødvendigt at generalisere
Newtons 2. lov, således at
det bliver en tensorlov. Den inertielle masse er da ikke en skalar, men derimod en tensor,
som vi kan kalde
inertimassetensoren.
Den generaliserede Newton-lov lyder da:
(6a) 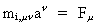
hvor 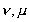 skal løbe
over rumkoordinaterne. Der skal summeres over skal løbe
over rumkoordinaterne. Der skal summeres over
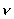 . Da den
universelle massefordeling omkring en partikels bane mest sandsynligt vil være
asymmetrisk, vil den inertielle
masse være anisotrop. Dette giver mulighed for en bekræftelse af
ovenstående, idet man meget
nøjagtigt skal måle en partikels inertielle masse, når denne
bevæger sig i forskellige
retninger. . Da den
universelle massefordeling omkring en partikels bane mest sandsynligt vil være
asymmetrisk, vil den inertielle
masse være anisotrop. Dette giver mulighed for en bekræftelse af
ovenstående, idet man meget
nøjagtigt skal måle en partikels inertielle masse, når denne
bevæger sig i forskellige
retninger.
Det bemærkes, at en partikels gravitationelle masse antages at være invariant
konstant.
Næste artikel
Hovedsiden
Louis Nielsen
Kommentarer kan sendes pr. E-mail til:
louis44nielsen@gmail.com
Tidligere publiceret:
- Louis Nielsen: Ny gravitationsteori (Gamma 9 Februar 1972, Tidsskrift
for fysik, Niels Bohr
Institutet, København).
- Louis Nielsen: En fotons bevægelse i et gravitostatisk G-felt (Gamma
17 Januar 1974)
- Louis Nielsen: Kosmologi baseret på kvantisering af rum og tid
(Fysisk Tidsskrift 77,
1979, no. 2, pp. 84-86)
- Louis Nielsen: Kvantisering af rum, tid og masse (Rostras Forlag 1983,
ISBN 87-88087-10-7).
Mit einem deutschen Resümee.
o.a.
SE&O
|
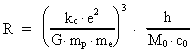
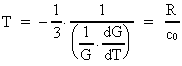
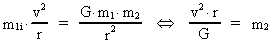
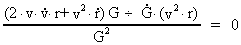
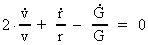
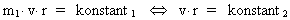
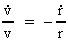
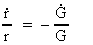
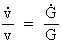
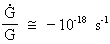
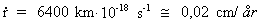
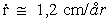
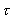 omkring sig selv til et bestemt
tidspunkt og den til dette tidspunkt hørende gravitations-
»konstant«. Da gravitations-»konstantens« størrelse
afhænger af universets
aktuelle alder, gives også en direkte sammenhæng med denne.
omkring sig selv til et bestemt
tidspunkt og den til dette tidspunkt hørende gravitations-
»konstant«. Da gravitations-»konstantens« størrelse
afhænger af universets
aktuelle alder, gives også en direkte sammenhæng med denne.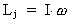
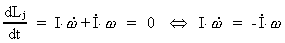
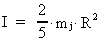
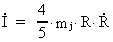
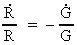
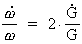
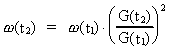
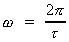
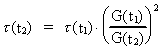
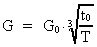
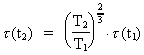
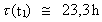
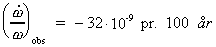
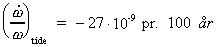
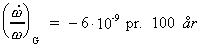
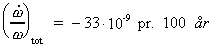
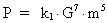
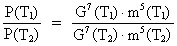
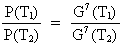
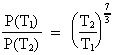
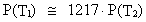
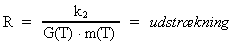
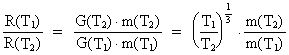
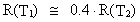
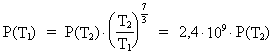
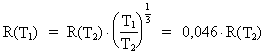
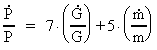
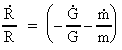
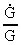 .
.
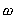 er vinkelhastigheden. Idet vi
antager, at impulsmomentet
holder sig konstant ved »oppustningen«, gælder der:
er vinkelhastigheden. Idet vi
antager, at impulsmomentet
holder sig konstant ved »oppustningen«, gælder der: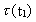 , som jorden
havde i devontiden for ca. 400 millioner år siden. Idet vi
benytter talværdierne:
, som jorden
havde i devontiden for ca. 400 millioner år siden. Idet vi
benytter talværdierne: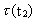 = 24 h
får vi:
= 24 h
får vi: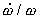 .
Den observerede værdi er angivet til:
.
Den observerede værdi er angivet til: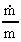 er aftagende funktioner med tiden,
ser man, at
er aftagende funktioner med tiden,
ser man, at 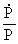 aftager med tiden,
og
aftager med tiden,
og 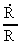 vokser med
tiden.
vokser med
tiden.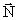 -felt-kraften og centrifugal- og
corioliskraften.
-felt-kraften og centrifugal- og
corioliskraften.
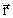 og vinkelhastighed
og vinkelhastighed
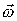 . Centrifugalkraftvektoren er
da givet ved:
. Centrifugalkraftvektoren er
da givet ved: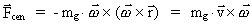
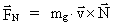
 den gravitationelle
masses hastighed i
den gravitationelle
masses hastighed i 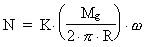
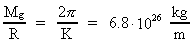
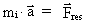
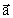 er accelerationen og
er accelerationen og
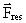 den resulterende kraft.
den resulterende kraft.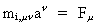
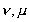 skal løbe
over rumkoordinaterne. Der skal summeres over
skal løbe
over rumkoordinaterne. Der skal summeres over
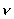 . Da den
universelle massefordeling omkring en partikels bane mest sandsynligt vil være
asymmetrisk, vil den inertielle
masse være anisotrop. Dette giver mulighed for en bekræftelse af
ovenstående, idet man meget
nøjagtigt skal måle en partikels inertielle masse, når denne
bevæger sig i forskellige
retninger.
. Da den
universelle massefordeling omkring en partikels bane mest sandsynligt vil være
asymmetrisk, vil den inertielle
masse være anisotrop. Dette giver mulighed for en bekræftelse af
ovenstående, idet man meget
nøjagtigt skal måle en partikels inertielle masse, når denne
bevæger sig i forskellige
retninger.