|
Af lektor cand. scient. Louis Nielsen Indledning I det følgende vil jeg fremlægge en teoretisk beskrivelse af vort kvantefysiske univers, – en beskrivelse hvor alle fysiske størrelser er kvantiseret. Min teori bryder med den gængse kvantemekaniske beskrivelse, der er baseret på bl.a. Erwin Schrödingers kontinuerte bølgeligning fra 1926. (Erwin Schrödinger (1887-1961): »Quantisierung als Eigenwertproblem«, Annalen der Physik, 79,489, (1926); 79,489, (1926); 80,437, (1926); 81,109, (1926).) Schrödinger selv mente, at den bølgemodel for kvanteprocesser i fysiske systemer, som bølgeligningen er udtryk for, blot er en matematisk nødløsning i mangel af en mere foreståelig kvantefysisk teori. I det følgende vil jeg vise, at det er muligt at give en mere forståelig og dermed rationel beskrivelse af universets kvantefysiske processer. Teorien er holistisk, idet det viser sig, at den mest fundamentale fysiske størrelse er den samlede stof-/energimasse i vort univers, eller hvad der er ækvivalent: den totale energi af hele vort univers! Som det vil blive vist, er energiindholdet af ethvert lokalt kvant en brøkdel af universets totale energi. Ethvert kvant er karakteriseret ved bestemte kvantetal, og enhver fysisk proces er karakteriseret ved kvantetalsændringer. For kvantetallene gælder visse nedre og øvre grænser, og ligeledes gælder der visse bevarelseslove. Hele min teori er baseret på den formodning, at der eksisterer en kvantisering af de fysisk fundamentale størrelser: rum, tid og masse. Min opdagelse af denne kvantisering og min opdagelse af kvantiseringens sammenhæng med Plancks konstant, lysets hastighed og universets samlede stof-/energimasse er også grundlaget for min holistiske kvantekosmologi med aftagende gravitation. Denne teori kan studeres andetsteds. Min generelle metode i den rationelle kvantefysik er ganske ligetil: Alle fysiske størrelser defineres med udgangspunkt i de fundamentale fysiske størrelser: Afstand, tidsinterval og masse. Som en konsekvens af disses kvantisering vil alle andre afledte fysiske størrelser også blive kvantiseret. Kvantisering af det fysiske rum, – dvs. et område hvori der eksisterer 'noget' i form af 'stof' og 'felter' og dermed energi – bevirker, at vi ikke i en fysisk beskrivelse af vort univers kan opretholde en kontinuert euklidisk geometri. Fysisk eksisterer der en mindste målestok – elementarlængden. Alle 'geometriske' forhold skal udmåles ved hjælp af denne elementare kvantelængde. Som følge af dette tyder det på, at geometriske forhold i mikrokosmos er 'kantede'. At dette virkelig er tilfældet, tyder meget i vor dagligdags og makroskopiske verden også på; tænk blot på de geometriske former af krystaller. Ligeledes vil selv den mest 'glatte' flade ved forstørring vise sig at være ru og dermed kantet. Vi lever åbenbart i et 'kantet' kvanteunivers! I det følgende viser jeg ved en simpel beregning, hvor meget energi der maximalt blev stillet til rådighed, da vort univers blev dannet. Jeg viser, at energiindholdet af et system kan beregnes som systemets ækvivalente masse multipliceret med lyskonstanten i anden potens. Det samme blev vist af Albert Einstein, men her vises det meget simplere.
Jeg giver også en omformning af den såkaldte Rydbergformel for hydrogenatomet,
idet jeg viser, at den kan omskrives til et udtryk, hvori der indgår diskontinuerte
kvantemasser. Fysisk kvantegeometri og rationel fysisk kvantemekanik Som en konsekvens af det fysiske rums kvantisering kan vi ikke opretholde den kontinuerte euklidiske geometri i vor beskrivelse af fysiske fænomener. I den fysiske kvantegeometri vil eksempelvis den euklidisk-pythagoræiske læresætning for en retvinklet trekant ikke gælde eksakt. Ej heller kan vi opretholde gyldigheden af det irrationelle tal pi, der angiver forholdet mellem en cirkels omkreds og diameter. I den fysiske kvantegeometri må vi indføre betegnelser som: kvantetrekanter og kvantecirkler osv. Da det viser sig, at det fysiske rumkvantum, kaldet elementarlængden, angivet i dagligdags praktiske måleenheder (f.eks. meter) er et uhyre lille tal, vil vi ikke i vor dagligdag observere konsekvenserne af en rum- og tidskvantisering. I den mikrofysiske verdensbeskrivelse vil rum- og tidskvantiseringen dog være signifikant relevant. Dette gælder ligeledes, når vi vil beskrive og forstå de allertidligste faser af vort univers. Generelt gælder en kosmisk fysisk kvantisering. Den fysisk mindste afstand i vort univers – elementarlængden – er givet ved brøkforholdet mellem Plancks konstant og produktet af universets samlede stof-/energimasse og lysets hastighed i feltfrit vacuum. Idet vi betegner elementarlængden med r0 gælder:
(1) 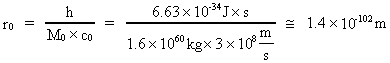 hvor h er Plancks konstant, M0 universets samlede stof-/energimasse og c0 lyskonstanten. Talværdierne af Plancks konstant og lyshastigheden er bestemt ved målinger i vore laboratorier. Talværdien af M0 er beregnet af en formel, som jeg har udledt i min kvantekosmologiske teori. Det mindste fysiske tidsinterval i vort univers – elementartiden – er givet ved brøkforholdet mellem elementarlængden og lyskonstanten:
(2) 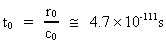 Elementartiden t0 er tidskvantet i vort univers. Elementarlængden og elementartiden angiver et absolut ruminterval og et absolut tidsinterval, forstået på den måde, at alle iagttagere uanset deres relative bevægelsestilstand vil 'måle' samme talværdier af elementarlængden og elementartiden. Dette ses af udtrykkene, der bestemmer r0 og t0. Alle iagttagere vil måle samme talværdier af h, c0 og M0.
Sagt med mere tekniske ord: r0 og t0 er invariante
over for en relativistisk Lorentz-transformation. Som noget nyt inden for den specielle
relativitetsteori sætter r0, t0 og
M0 nedre og øvre grænser for talværdierne af
transformerede længder,
tidsintervaller og masser! Disse begrænsninger sætter os meget
interessant i stand til at udlede en bestemt masses Compton-længde,
se senere! I øvrigt kræver rum-tidskvantisering, at de
relativistiske Lorentz-transformationer også kvantiseres,
således at det bliver transformationsligninger mellem rum- og
tidskvantetallene. Disse rum- og tidskvantetal er bestemt ved følgende
krav: Enhver endelig fysisk afstand
(3) 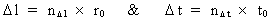
hvor
Kvantecirklen og det rationelle pi I den fysiske kvantegeometri vil en 'cirkel' være kvantiseret, dvs. 'kvantecirklen' vil være en polygon, hvor sidelængderne alle er lig elementarlængden. Dette betyder, at kvantecirklens omkreds O er lig med et rumkvantetal nO multipliceret med r0. Ligeledes gælder der, at 'diameteren' d i kvantecirklen er lig med et rumkvantetal nd multipliceret med r0. Der gælder altså for forholdet O/d:
(4) 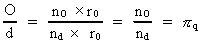 Det bemærkes, at d er den gennemsnitlige kvantediameter i en fysisk fluktuerende kvantecirkel.
I ligning (4) definerer brøken mellem de to rumkvantetal et rationelt
tal. Dette tal vil jeg kalde det rationelle pi og betegne det med
Kvantekinematik og kvantedynamik. Diskontinuert bevægelsesfysik En konsekvens af rum-tidskvantiseringen er, at en partikels hastighed og acceleration også er kvantiserede størrelser. Alle andre fysiske størrelser, der er afledt fra de fundamentale fysiske størrelser – afstand, tid og masse –, vil også være kvantiserede. Det skal bemærkes, at en partikel her betyder en fysisk partikel, dvs. en 'fluktuerende' kugle – en kvantekugle – med gennemsnitlig udstrækning lig med elementarlængden multipliceret med et naturligt tal. Inden for denne kvantekugle kan der være koncentreret en vis energimængde svarende til, at partiklen har en bestemt 'stofmasse'. At kuglen er 'fluktuerende' eller 'sløret' betyder, at vi fysisk betragtet kun er i stand til at måle en fysisk størrelse inden for en vis mindste usikkerhed i overensstemmelse med Heisenbergs usikkerhedsrelationer. Lad os nu definere en partikels hastighed v i forhold til et bestemt referencesystem. Vi definerer:
(5) 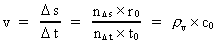
hvor
I definitionsligningen (5) er
Hvis partiklen påvirkes af en kraft, dvs. en fysisk påvirkning, der er i stand til at give partiklen en hastighedstilvækst, altså en acceleration, da vil vi definere partiklens acceleration a således:
(6) 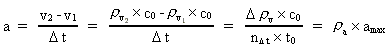
I denne definitionsligning kan vi kalde
Vi kan nu udvikle en kvantedynamik, idet vi vil definere de mekanisk
fysiske størrelser på samme måde som i den klassiske
newtonske mekanik. Definition af kvantekraften Vi vil definere en fysisk kraft som 'noget', der er i stand til at give en partikel en acceleration målt i forhold til et bestemt referencesystem. Vi vil definere størrelsen F af den kraft, der kan give en partikel en acceleration a i overensstemmelse med Newtons 2. lov, dvs.:
(7) 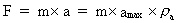
hvor m er partiklens masse. Definition af en krafts arbejde og energiomsætning
Hvis en partikel forskydes over en strækning
(8) 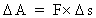 Dette udtryk gælder kun, hvis kraftretningen er parallel med forskydningsretningen. Ifølge definitionerne for begreberne arbejde og energi er et udført arbejde på en partikel ensbetydende med, at partiklen enten får tilført en vis energimængde – arbejdet er da positivt – eller også fratages der partiklen energi, – og arbejdet på partiklen er da negativt.
I øvrigt vil vi vedtage: Et system, der på en eller anden måde
( –måske på os endnu ukendt måde –) er i stand til at
udføre et positivt arbejde, siges at indeholde energi. Og for at gentage:
Et udført arbejde er ensbetydende med overførsel af energi fra et system
til et andet system. Universets totale energiindhold og dets nuværende fordeling Af ligningerne (7) og (8) kan vi beregne den totale energimængde, der er til rådighed i vort univers, og som blev dannet eller udløst, da universet foretog det første kosmiske kvantespring for omkring 11 milliarder år siden. En formél beregning giver følgende:
(9) 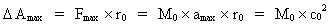 Udtrykket angiver det maximale arbejde, der omsættes ved det første kosmiske kvantespring over en strækning lig med elementarlængden r0.
I ligningsudtrykket (9) er M0 universets samlede masse. Universets
totale energiindhold kan således beregnes som produktet af dets totale masse
multipliceret med lyskonstanten i anden potens. Meget interessant er dette den samme beregningsformel, som Albert Einstein udledte i den specielle relativitetsteori i 1905, den berømte formel, der sammenknytter energi og masse som ækvivalente størrelser – to størrelser, der ytrer sig som to sider af samme grundfysiske størrelse. Da universet under dets udvikling deles op i mindre og mindre stof-/energikvanter, følger det umiddelbart, at en bestemt 'masse' må svare til et energiindhold Em beregnet efter følgende formel:
(10) 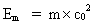 hvor m er det betragtede 'systems' masse. I min holistiske kvantekosmologi udledes følgende kvantekosmologiske ligning:
(11) 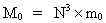 hvor m0 er universets nuværende elementarmasse, og hvor N³ er et evolutionskvantetal, hvis nuværende talværdi angiver antallet af det nuværende antal elementarkvanter. N er lig med forholdet mellem universets begyndelsesgravitations-'konstant' G0 og dets nuværende gravitations-'konstant' G. Ved multiplikation med c0² på begge sider af ligning (11) fås:
(12) 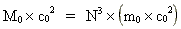
Ligning (12) er en energibevarelseslov, der blot udtrykker, at den totale
energi, der er til rådighed i vort univers i dag, er fordelt ud
på elementarkvanter!
Holistisk kvantebeskrivelse af hydrogenatomets liniespektrum
En fotons kvanteenergi
I år 1900 måtte den tyske fysiker Max Planck (1858-1947) [Max Planck:
»Über das Gesetz der Energieverteilung im Normalspektrum«, Annalen der
Physik, 4,553, (1901)] 'tvinges' til at kvantisere den elektromagnetiske
strålingsenergi, der blev udsendt fra et såkaldt 'absolut sort legeme'.
Dette var den absolut eneste måde, hvorpå han kunne 'forklare' de
eksperimentelle data. Max Planck indså – men meget mod sin
vilje!, at elektromagnetisk strålingsenergi er kvantiseret i 'energiklumper'
– kaldet fotoner.
Den enkelte fotons energi kan beregnes af formeludtrykket:
(13) 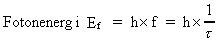
hvor h er Plancks konstant, f er den ækvivalente
strålingsfrekvens, og I den klassiske beskrivelse af elektromagnetisk stråling antages den at være et kontinuert fænomen, hvor alle mulige reelle frekvenstal er mulige. Man sætter endog ingen øvre talgrænser! I den her fremlagte holistiske kvantefysik kan det hele beskrives mere rationelt og med universets totale energi som en yderst fundamental størrelse. Vi kan omskrive formeludtrykket (13) på følgende måde:
(14) 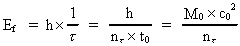
I dette udtryk er t0 elementartiden og
Vi kan således konstatere: En fotons energiindhold er en hel brøkdel
af universets totale energi! Hydrogenatomets Rydbergformel omformet til en universel kvantelov For at systematisere talværdierne af de bølgelængder, man eksperimentelt havde udmålt for hydrogenatomets synlige liniespektrum, 'konstruerede' den schweiziske matematiker Johan Jakob Balmer (1825-1898) i 1885 den såkaldte Balmerformel. Denne blev i 1890 generaliseret af den svenske fysiker Johannes Rydberg (1854-1919). Denne Rydbergformel kan skrives som:
(15) 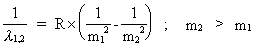
I denne formel er
Som den danske fysiker Niels Bohr (1885-1962) viste i 1913, er højresiden i Rydbergformlen knyttet til kvanteprocesser i det fotonudsendende atom. Niels Bohr kunne teoretisk udregne talværdien af Rydbergkonstanten ved hjælp af de målte talværdier af Plancks konstant, elektronens masse og elektriske ladning og lysets hastighed. Vi kan omskrive Rydbergformlen til en energiformel ved at multiplicere med h • c0 på begge sider af lighedstegnet i ligning (15). Vi får da:
(16) 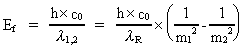
idet vi også har indført den reciprokke værdi af
Rydbergkonstanten
(17) 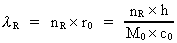 Idet vi indsætter udtrykket i ligning (17) i ligning (16), får vi:
(18) 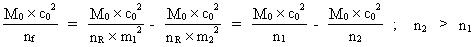 hvor vi også har benyttet kvanteudtrykket for en fotons energi Ef = (M0 • c0²) / nf Af ligning (18) ser vi følgende: Alle leddene angiver en hel brøkdel af universets totale energi. Hvis vi dividerer på begge side af ligningen med c0², angiver alle leddene en hel brøkdel af universets totale masse. Vi kan derfor også skrive ligningen udtrykt ved massestørrelser:
(19) 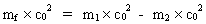
(20) 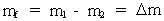 Massen på venstre side af ligningen angiver massen af en udsendt foton, og højre side af ligningen angiver en massetilvækst af det system, der udsender en foton. Massetilvæksten af systemet er naturligvis negativ. Vi kan sluttelig også dividere ligningen med M0 • c0² og får da en ligning udelukkende mellem kvantetal – kvantetal, der karakteriserer den udsendte foton og kvantetilstande af det system, der udsender en foton. Som det kan ses, udtrykker Rydbergformlen og dens omskrivninger blot energibevarelsesloven! I dette afsnit startede vi med Rydbergs formel, der specifikt kun gælder for et hydrogenatoms strålingsudsendelse. Den omformede formel (19) må formodes at have almen gyldighed, idet den er udtryk for en universel lovmæssighed – nemlig energibevarelse. Kvantetalsligningen kan skrives:
(21) 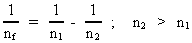
hvor nf er fotonkvantetallet.
26/12-1996
Louis Nielsen Næste artikel
|
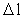 er givet ved et naturligt
tal multipliceret med elementarlængden r0.
Ethvert endeligt fysisk tidsinterval
er givet ved et naturligt
tal multipliceret med elementarlængden r0.
Ethvert endeligt fysisk tidsinterval
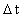 er givet ved et naturligt
tal multipliceret med elementartiden t0. Dvs. der
gælder følgende:
er givet ved et naturligt
tal multipliceret med elementartiden t0. Dvs. der
gælder følgende: 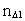 er
rumkvantetallet, og
er
rumkvantetallet, og
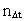 er
tidskvantetallet.
er
tidskvantetallet.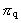 .
I praktiske talberegninger spiller det ingen rolle, om pi er et rationelt
tal eller et irrationelt tal, idet vi alligevel afrunder vore talfacit til
et antal signifikante decimaler. Ved fysikteoretiske analyser er det dog
relevant at vide, at rummet er kvantiseret.
.
I praktiske talberegninger spiller det ingen rolle, om pi er et rationelt
tal eller et irrationelt tal, idet vi alligevel afrunder vore talfacit til
et antal signifikante decimaler. Ved fysikteoretiske analyser er det dog
relevant at vide, at rummet er kvantiseret. 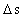 er den strækning, der
tilbagelægges i tidsintervallet
er den strækning, der
tilbagelægges i tidsintervallet
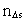 rumkvantetallet og
rumkvantetallet og 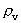 . Dette hastighedskvantetal
ligger i talintervallet mellem nul og en, idet en partikel aldrig kan bevæge
sig med en hastighed, der er over c0.
. Dette hastighedskvantetal
ligger i talintervallet mellem nul og en, idet en partikel aldrig kan bevæge
sig med en hastighed, der er over c0. 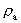 accelerationskvantetallet, der ses at være et rationelt tal.
Dette accelerationskvantetal ligger også i talintervallet mellem nul
og en. Brøkforholdet mellem lysets hastighed og elementartiden
c0 / t0 giver en fysisk øvre
grænse
for en partikels acceleration. Denne øvre grænseacceleration
betegnes med amax.
accelerationskvantetallet, der ses at være et rationelt tal.
Dette accelerationskvantetal ligger også i talintervallet mellem nul
og en. Brøkforholdet mellem lysets hastighed og elementartiden
c0 / t0 giver en fysisk øvre
grænse
for en partikels acceleration. Denne øvre grænseacceleration
betegnes med amax.
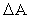 af det udførte arbejde
vil vi definere ved udtrykket:
af det udførte arbejde
vil vi definere ved udtrykket:
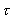 den
ækvivalente svingningstid.
den
ækvivalente svingningstid.
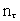 et naturligt
tidskvantetal.
et naturligt
tidskvantetal.
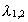 en bestemt
spektrallinies bølgelængde.
m1 og m2 er naturlige tal, hvor
m2 > m1. R er den såkaldte
Rydbergkonstant med den målte talværdi
R = 1.097 · 107 meter -1.
en bestemt
spektrallinies bølgelængde.
m1 og m2 er naturlige tal, hvor
m2 > m1. R er den såkaldte
Rydbergkonstant med den målte talværdi
R = 1.097 · 107 meter -1.
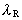 = 1/R, der
angiver en længde, vi kunne kalde Rydberglængden.
Denne fysiske længde er lig med et naturligt tal nR
multipliceret med elementarlængden r0 :
= 1/R, der
angiver en længde, vi kunne kalde Rydberglængden.
Denne fysiske længde er lig med et naturligt tal nR
multipliceret med elementarlængden r0 :