Indledning

I det følgende vil jeg vise, at der eksisterer en intim — holistisk — sammenhæng mellem mikrokosmos — atomernes verden — og makrokosmos – universet som helhed. Jeg udleder formler der sætter os i stand til at beregne kosmologiske størrelser, såsom universets alder, udstrækning og totale masse ved hjælp af atomfysiske størrelser og Newtons gravitationskonstant. Disse størrelser er for de flestes vedkommende målt med stor nøjagtighed. Den eneste størrelse, der endnu ikke er målt med stor nøjagtighed, er elektronens udstrækning, dog menes den at være af størrelsesordenen under 10^—18 m. De udledte formler er baseret på min opdagelse af to formelsammenhænge — ligning (1) og ligning (2) — der sammenknytter fysiske størrelser fra mikrokosmos, eksempelvis Plancks konstant, elektronens masse, dens udstrækning og elektriske ladning og størrelser, der er karakteristiske for universet som helhed, såsom dets masse, udstrækning og alder. Hertil kommer lysets hastighed og Newtons gravitationskonstant. De opdagede formler indgår i min kvantekosmologi, der har hovedtitlen: 'Holistisk kvantekosmologi med aftagende gravitation'. Afhandlingen findes på Internet under adressen: http://louis.rostra.dk/.

Den kosmologiske grundligning

Da min opdagede formel i (1) giver en sammenknytning mellem størrelser, der kendetegner mikrokosmos, og størrelser, der kendetegner makrokosmos, har jeg kaldt den for den kosmologiske grundligning:

(1)

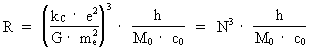
I ligning (1) er R universets aktuelle udstrækning, k_C coulombkonstanten, e elektronens elektriske ladning, m_edens masse, G Newtons gravitations'konstant', h Plancks konstant, c₀lysets hastighedog M₀universets samlede stof/energimasse. Brøken i den første parentes, betegnet med N = 4,16 · 10⁴², angiver forholdet mellem de elektrostatiske kræfter og gravitostatiske kræfter mellem to elektroner. Brøkforholdet mellem Plancks konstant og produktet af universets samlede masse og lyshastigheden angiver den fysisk mindste afstand i universet og kaldes derfor elementarlængden.
Talværdien af R er — også i den etablerede kosmologi — bestemt til at være af størrelsesordenen 10²⁶m og M₀ er i min kvantekosmologi beregnet til omkring 1,6·10⁶⁰ kg, en talværdi jeg beregner ud fra en 'målt' relativ variation af Newtons gravitations’konstant’.

Forholdet mellem elektronens massedensitet og universets massedensitet

Lad os beregne brøkforholdet mellem en elektrons massedensitet og den gennemsnitlige massedensitet af universet :

(2)

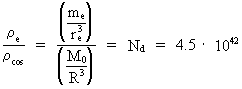
I (2) er benyttet følgende talværdier: R = 10²⁶ m ; r_e =0,5·10^—18 m ; m_e = 9,11·10^—31 kg; M₀ = 1,6·10⁶⁰ kg.
Vi ser yderst interessant, at tallet N_der ganske tæt på talværdien af N. Dette kan ikke være en tilfældighed!!! Med mere nøjagtige talværdier er jeg ret sikker på, at N_d er lig med N. At der eksisterer en sammenhæng mellem universets middelmassedensitet, elektronens massedensitet og størrelsen N er en logisk følge af universets udvikling fra et mindre og mere tæt univers til et voksende og mindre tæt univers. Størrelsen N er ikke konstant, men spiller rollen som et kosmisk evolutionskvantetal, der havde en meget mindre talværdi, dengang elektroner blev dannet i det unge univers. Elektroner — og dermed alt stof — er 'rester' fra det tidligste univers, der endnu ikke er gået i opløsning. (Se ovenstående URL). Idet jeg antager, at N_d = N, ser vi, at der eksisterer en sammenhæng mellem størrelserne i ligning (1) og størrelserne i ligning (2). Opdagelsen af sammenhængen er ganske rigtigt fundet ved hjælp af nogle kendte talværdier af R og M₀ , men med den opdagede sammenhæng kan R og M₀ omvendt beregnes ved atomfysiske størrelser og Newtons gravitations'konstant'!

Beregning af universets udstrækning, alder og masse

Ved sammenkobling af (1) og (2) kan universets udstrækning R beregnes af følgende formel:

(3)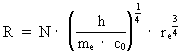

Hvis man for elektronens udstrækning r_e benytter talværdien 0,5·10^—18 m fås for R:

(4)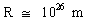

hvilket naturligvis ikke er overraskende.

R kan også skrives som:

(5)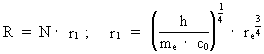

hvor r₁angiver en karakteristisk længde: r₁ = 2,4 · 10^–17 m
Universets alder T kan beregnes af formlen:

(6)

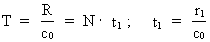
hvor t₁ angiver et karakteristisk tidsinterval: t₁ = 7,8 · 10^–26 s.
Størrelsen h/(m_e·c₀) angiver i øvrigt elektronens ’Compton bølgelængde’.
Universets masse M₀ kan beregnes af følgende formel:

(7)

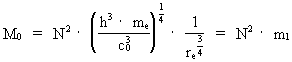
hvor m₁ er en karakteristisk masse: m₁ = 9,2 · 10^–26 kg.

Aftagende gravitation og den voksende elektron

Af de udledte formler ses det, at med et expanderende univers, hvor R bliver større og større, må nogle af de indgående størrelser variere, efterhånden som universet udvikler sig. Spørgsmålet er da: Hvilke af størrelserne varierer? Meget tyder på, at G aftager med universets udvidelse. Dette er behandlet i min kvantekosmologi, hvor det også antages, at universets masse holder sig konstant. Da det også antages, at elektronens masse er konstant, fører dette til, at elektronens udstrækning må variere, efterhånden som universet udvider sig. Beregningerne viser (se ovenstående reference), at elektronens udstrækning forøges. Med andre ord: Elektronen vokser! For den tidslige relative tilvækst af elektronens udstrækning gælder der følgende:

(8)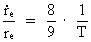

hvor T er universets aktuelle alder. Vi ser af ligning (8), at det relative 'vokseværk' af elektronen i vor epoke er yderst lille, omkring 8,5·10^–11 pr. år. I tidligere epoker af universet foregik forøgelsen hurtigere. Med andre ord har elektronen været mindre, da universet var yngre. Dette forekommer også at være en logisk udvikling, thi hvordan kunne der ellers være plads til elektroner i det allertidligste og uhyre meget mindre univers? Hvis man stiller spørgsmålet: Varierer protonens og andre sammensatte partiklers udstrækning også, efterhånden som universet ekspanderer? Da er svaret: Ja!

© Louis Nielsen, 20. nov. 1997

  Næste artikel